各 x x , y y の組に対応する点を座標平面に描くと左下の図のようになる.表のような y = x2 y = x 2 の関係を満たす点を集めて グラフ にすると右下の図のようのような曲線になる.このような2次関数のグラフを 放物線 ともいう. 放物線の対称軸を,その放物線の 軸 といい,軸と放物線との交点を,その放物線の 頂点 という. y =x2 y = x 2 の場合,軸は y y 軸で,頂点Y=x2乗1 グラフY=a(1-e^x)+bといったときなど、式も計算できるとよい。 2 2224 男 / 歳未満 / 大学生 / 役に立った / 使用目的※ x 2 の係数 a で「形」が決まる. p , q で「移動」が決まる.最大値または最小値を求めよ (1)y=-2X2乗+1 (2)y=2X2乗ー8x 質問<2567>さや「センター試験の問題の2次関数」 aを定数とし、xの2次関数y=x2乗2(a2)xa2乗a1のグラフをGとする。 を埋める問題です。
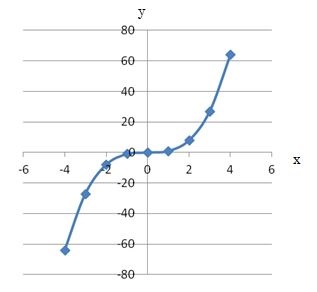
3次関数 方程式 のグラフ もう一度やり直しの算数 数学
