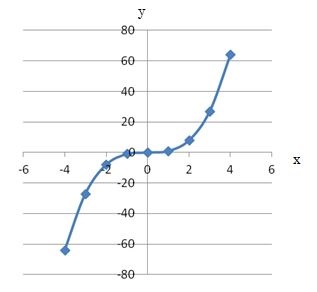
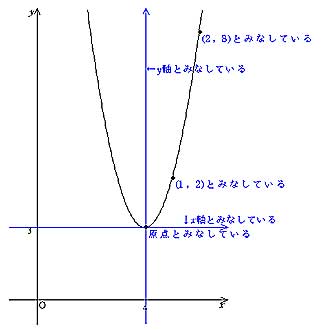
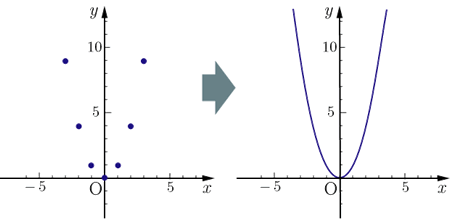
各 x x , y y の組に対応する点を座標平面に描くと左下の図のようになる.表のような y = x2 y = x 2 の関係を満たす点を集めて グラフ にすると右下の図のようのような曲線になる.このような2次関数のグラフを 放物線 ともいう. 放物線の対称軸を,その放物線の 軸 といい,軸と放物線との交点を,その放物線の 頂点 という. y =x2 y = x 2 の場合,軸は y y 軸で,頂点Y=x2乗1 グラフY=a(1-e^x)+bといったときなど、式も計算できるとよい。 2 2224 男 / 歳未満 / 大学生 / 役に立った / 使用目的※ x 2 の係数 a で「形」が決まる. p , q で「移動」が決まる.最大値または最小値を求めよ (1)y=-2X2乗+1 (2)y=2X2乗ー8x 質問<2567>さや「センター試験の問題の2次関数」 aを定数とし、xの2次関数y=x2乗2(a2)xa2乗a1のグラフをGとする。 を埋める問題です。
3次関数 方程式 のグラフ もう一度やり直しの算数 数学
Y=x2乗-4x+3 グラフ
Y=x2乗-4x+3 グラフ-中3数学。2乗に比例する関数(y = ax²)の「変域」を求めなさい。うわ、変域って何? 頂点が最小? 分からん(ガクッ)倒れ込む中学生。立て、立つんだトォォォォ~ッ! オール5家庭教師、見参ッ! グイグイ成績が上がる数学のコツ。無料サイトだ。2.2次関数のグラフ (1) 2次関数のグラフは,放物線とも呼ばれ,ボールを遠投したとき描く曲線のような形をしています。 その曲線を式で書くと,y=ax2 (a≠0) の形に書かれます。 この章では,この曲線について,前の章で学んだ平行移動を行なうことにします。 まず,y=ax2 の性質と,これから使う名称について説明しておきます。 a は 0 以外の適当な数ですが



Y X 2 2x 1のグラフあってるでしょうか 解説のグラフと Yahoo 知恵袋
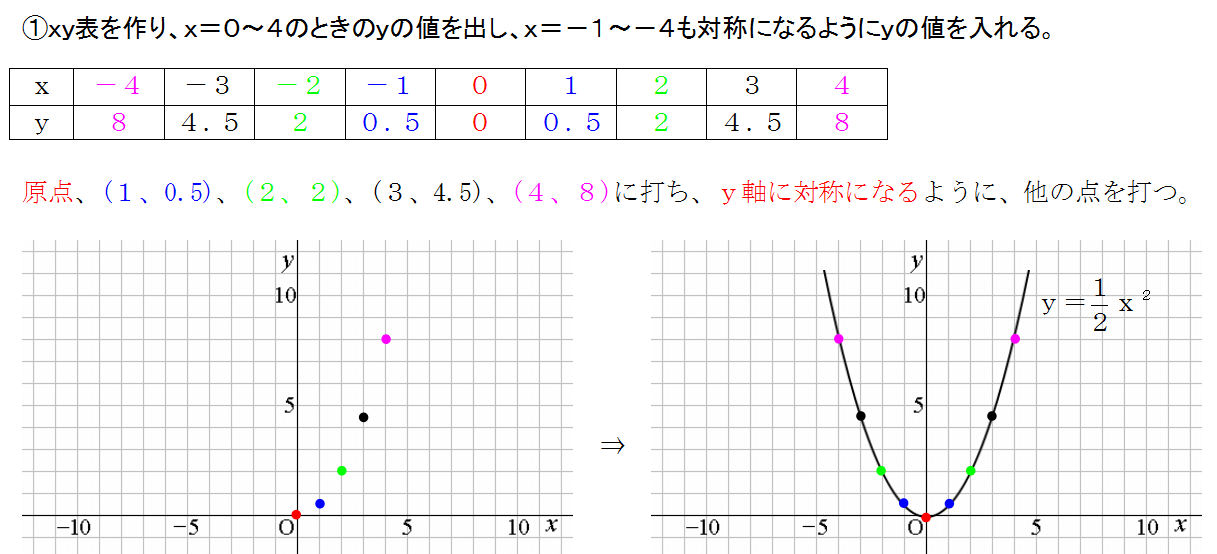
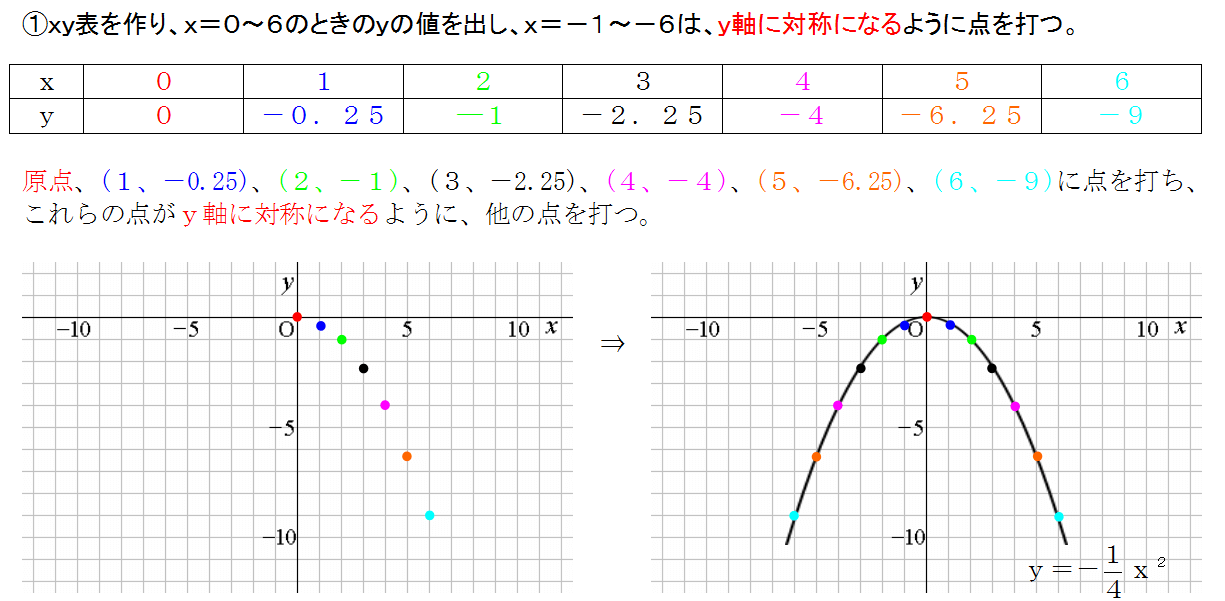
二次関数 y = x^2 (「2乗」をこう書きます)は「下に凸」なので、「頂点」で最小になります。 つまり「x=3 が頂点」ということです。関数グラフ GeoGebra x y z π 7 8 9 ×7221 2乗に比例する関数 グラフ グラフの描き方 2乗に比例する関数のグラフは直線ではないため、 できるだけたくさんの点をとりフリーハンドでなめらかな曲線のグラフをかく。 y= 1 4 x 2 のグラフの書き方 xの値を式に代入して文献 ・『岩波数学入門辞典』平方根(p543) ・吉田
Y軸について対称である。 a > 0のときは上に開き、a < 0のときは下に開く。 aの絶対値が小さいほどグラフの開きが大きい。 y=ax 2 のグラフとy=ax 2 のグラフはx軸について対象である。 2乗に比例する関数 グラフ 例題と練習問題 練習問題 2乗に比例する関数2Y = ax2 y = a x 2 の関係にある数量を、表、式で表したり、変数の変域、変化の割合を求めたり、曲線上の2点を通る直線の式を求めることができる 関数 y = ax2 y = a x 2 ・変化の割合の意味,関数 y = ax2 y = a x 2 のグラフの特徴,直線の式の求め方を理解する 本時の目標1変数関数 y=f (x)=x2 の性質 :トピック一覧 ・ グラフ / 増減 / 値域 / 有界性 / 最大最小 / 逆像 (平方根および√) / 単射 / 全射 / 全単射 / 逆関数 / 極限 / 連続 /極大極小 ・ 平方根と√の定義 ※ 1変数関数の具体例: y=x / y=x3 / y= 1/ x → 自然数指数の冪関数 / 整数指数のべき関数 / 有理数指数のべき関数 / 実数指数のべき関数 定数値関数 / 比例 / 一次関数 / 二次関数
カイ2乗分布(グラフ) 12 /2件 表示件数 5 10 30 50 100 0 1 1547 男 / 40歳代 / 教師・研究員 / 役に立った / 使用目的 自由度の大きさに応じてカイ自乗分布の形がどのように変化していくかを初学者に示す際に役立った 2 1627 女 / 50歳代定義:回転放物面 2変数関数 z = f (x,y) = x2 y2 の グラフ すなわち、 z = f (x,y) = x2 y2 を満たす ( x, y, z) を全て集めた集合 { ( x,y, z) z=x2 y2 } は、 以下のようになる。 このグラフを、 回転放物面 と呼ぶ。 文献 ・高橋『 微分と積分2 』§31例32 ( p 64)Y = x 2という式をエクセルに渡しても理解しません 代わりに y = x 2という式を使った数値の表を作成して、それをグラフにします セル に 0 、セルB2 に=^2 と入力します。 キャレット ^は一般的な Windows キーボードの右上の方にあります、詳しくは →



二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師



Y x2乗 4x 4のグラフってどうなりますか 頂点と軸と凸 Yahoo 知恵袋
中3数学。2乗に比例する関数 (y = ax²)。この a は「変化の割合」? xの値が「0から2まで」増加する? 分からん(ガクッ)倒れ込む中学生。立て、立つんだトォォォォ~ッ! オール5家庭教師、見参ッ! 2次関数のコツ、成績アップ法を公開。Téléchargés √ y=x2乗 グラフ Y=x2乗1 グラフ ≪解説≫ y=x 2 ,y=2x 2 ,y=3x 2 などのようにy=ax 2 の形で書かれる関数を,yがxの2乗に比例する関数といいます.15 ベストアンサー x2乗+ (y 3√x2乗)2乗=1 とありますが,3は係数ではなく 正しい式は x² (y∛x²)²=1 ① で,♡を描きたいのでしょう. ①は陰関数ですが, dy/dx=0 という方程式の実数解を正確に求めることができなければ,増減の様子が分からず,微分法を用いてグラフを描くことはできません. 実際にその計算を行ってもらえばよいのですが 計算は困難




基本 無理関数のグラフ 放物線の一部 なかけんの数学ノート



定積分で面積を求める x軸と曲線 直線 一歩一歩ぐんぐんブログ
指数関数④ y=e x² のグラフ(正規分布曲線もどき) 定義域は全ての実数なので,\ 記述の必要はない 対称性は,\ f (x)=e^ { (x)²}=e^ {x²}=f (x)より,\ {偶関数 (y軸対称)}である f' (x),\ f" (x)は常にe^ {x²}>0より,\ それぞれ2x,\ 2 (12x²)だけで符号が決まる x0との y=ax2乗のグラフで覚えておきたい用語 まず、グラフの形は 放物線 となります。 この放物線は左右対称の形となっており、その折れ目となる線のことを 軸 といいます。 指数関数 先ほど、 y = 2x y = 2 x のグラフを見ました。 このような、 y = ax y = a x という形をした関数を、 指数関数 (exponential function) と言います。 指数の部分に x x がある関数、ということですね。 なお、このとき、 a a には2つの条件が付きます。 1つは




基本 指数関数のグラフ なかけんの数学ノート
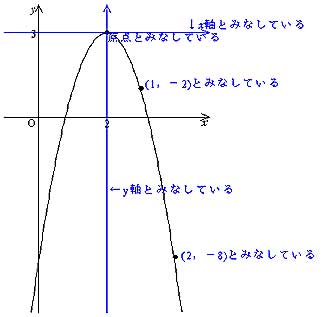



授業実践記録
そうすれば、このようにグラフが完成します(^^) 分数がでてきて困ったときには 無視する! これがポイントですね(^^) y=ax2乗のグラフ書き方 まとめ お疲れ様でした! 放物線のグラフを書くためには 丁寧に点を取って、それらをなめらかーに結ぶ!グラフ y=1/2x^2 y = 1 2 x2 y = 1 2 x 2 1 2 1 2 と x2 x 2 を組み合わせます。 y = x2 2 y = x 2 2 与えられた放物線の性質を求めましょう。 タップしてもっと手順を表示する Rewrite the equation in vertex form タップしてもっと手順を表示する x 2 2 x 2 2 を平方完成します。 二次関数y=a (xp)^2のグラフ 例として、 y = x2 y = x 2 のグラフを x 軸方向に 1 1 だけ移動したものを考えてみます。 グラフは次のようになります。 グレーが移動前、黒い太線が移動後のグラフです。 各点の移動に注目して、グラフを見ながら点の座標をいく




2次関数のグラフと直線



授業実践記録
2乗に比例するグラフ y=ax 2 のグラフをかいてみましょう。 aの値によって、グラフはどのようになるでしょうか。 y=x 2 のグラフ(青色)も、y=2x 2 のグラフ(緑色)も放物線になります。 比例定数が大きいほうがグラフは細長くなります。 なぜなら、x の値に対応する y の値が大きくなるからです。 放物線が y=ax 2 で表されるとき、点(3,18)を通る放物線の関数 y= f(x) 上の点 ( a, f(a) ) における法線の方程式は y−f(a) = − (x−a) (解説図) −−−−−−−− 接線の傾きが m = f'(a) であるとき,これに垂直な法線の傾きは,二直線の垂直条件 mm'=−1 から求めることができます。 すなわち,法線の傾きを m' とすると,図の放物線lはy= 1 2 x 2 の グラフで、放物線mはy=ax 2 のグラフである。lとmがx軸に平行な直線nと交わる点をそれぞれA, Bとする。Aのx座標が4, Bのx座標が2のとき、aの値を求めよ。



Q Tbn And9gcr5xwf9edrcskejqgyagxfwhnmwvaa7xrvtcx Jl9p Kp5wcn6m Usqp Cau
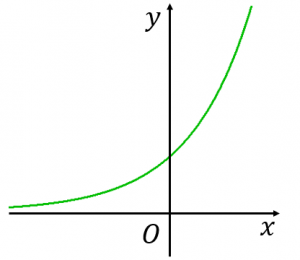



Y E Xのグラフをきれいに書く6つのコツ 具体例で学ぶ数学
2次関数の入試問題1 → スg スム版は別包ソス ス ス スi ス ス スホ費ソスj スQ ス ス スヨ撰ソス スフグ ス ス スt スm スW ス ス ス` スn → ス ス ス スpPDF スナは別包ソス y= (x p) 2q スフグ ス ス スt ス ス y=x 2 スフグ ス ス スt ス ス x ス ス スフ撰ソス スフA x 2 b x c a x 2 b x c の形を使い、 a a, b b, c c の値を求めます。 a = 1 4, b = 0, c = 0 a = 1 4, b = 0, c = 0 放物線の標準系を考えてみましょう。 a ( x d) 2 e a ( x d) 2 e Substitute the values of a a and b b into the formula d = b 2 a d = b 2 a d = 0 2 ( 1 4) d = 0 2 ( 1 4) 右側を簡略化し 発展問題もアリ! |中学数学・理科の学習まとめサイト! y=ax2乗aの求め方についてパターン別に解説! 発展問題もアリ! を求めろって言われても 何をすればいいの! ? というわけで、今回の記事では中3で学習する関数 の単元から「 の求め



2乗に比例するグラフ 中学から数学だいすき



7 演習 関数グラフ表示ソフトgrapes
グラフの縮小率: (0~1推奨) 指数関数のグラフ y=() 数式直接入力 y= x 25は、{x^2}5と書きます。 例:y={(1/2)^x}1(2分の1のx乗プラス1) 使い方 式の入力には、数字と「x * / ( ) { }」を使用します。すべて半角です。 ×は「*」、÷は「/」を用います。



ベストyx2乗1 グラフ 最高のぬりえ




基礎数学 5回目
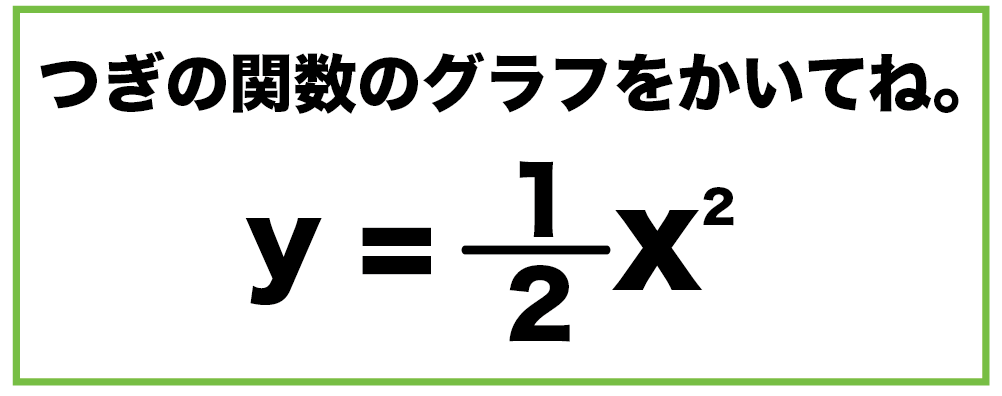



中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



Y X 2 2x 1のグラフあってるでしょうか 解説のグラフと Yahoo 知恵袋
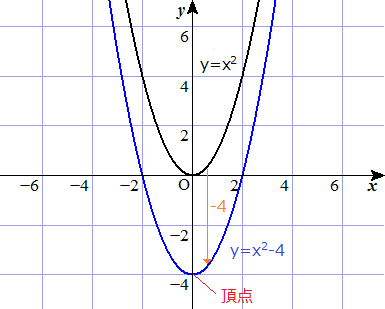



例題で学ぶ高校数学 Y Ax2 Q




4乗のグラフ 2乗のグラフは学校で習いました 4乗のグラフはどんな 数学 教えて Goo




基礎数学 6回目




2次関数 変域 変域からの式の決定 基 標 数学の解説と練習問題




練習36教えてください また例19のとこのグラフがわかりません Clear



3次関数はどうなる 中学から数学だいすき



図のように関数y X2乗とy Ax Bのグラフが 2点a Bで交わ Yahoo 知恵袋




中学校数学 3年生 数量 2乗に比例する関数 Wikibooks




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ




中学校数学 3年生 数量 2乗に比例する関数 Wikibooks



二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師
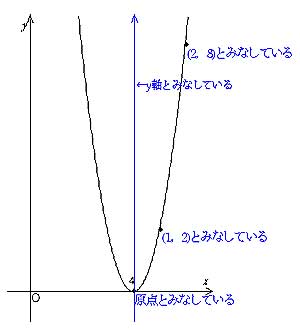



授業実践記録




2次関数 Y A X P のグラフの書き方 グラフの平行移動 数学i By ふぇるまー マナペディア



二次関数のグラフ




Y 1 X 2乗 4 写真が分かりやすいと思います の増減 凹凸な Y 1 数学 教えて Goo
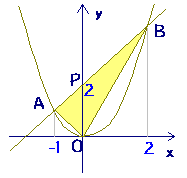



2次関数のグラフと直線



Y 1 X2乗のグラフ Youtube




中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく




基本 二次関数 Y Ax 2 のグラフ なかけんの数学ノート



1
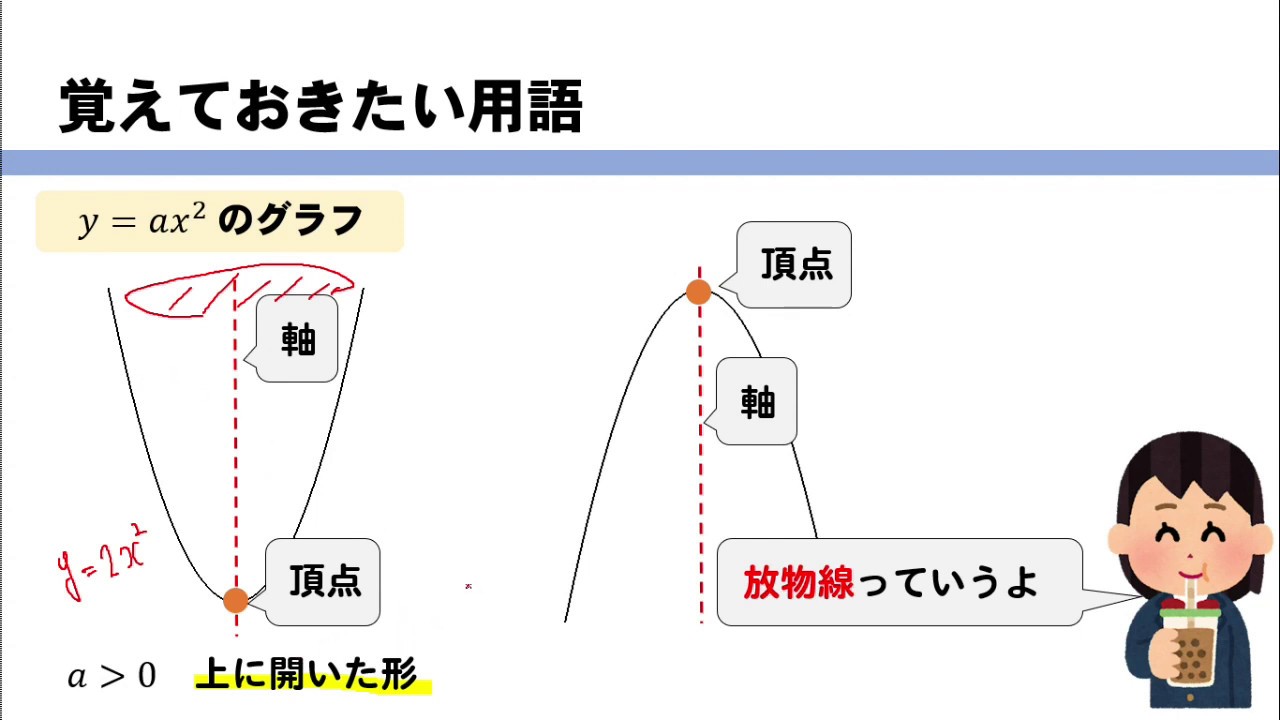



関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ



二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師



無料でダウンロード 関数 Yx2乗 ニスヌーピー 壁紙




例題で学ぶ高校数学 Y A X P 2



因数分解とグラフ 中学から数学だいすき



Y X2乗 4の式で頂点と軸を求めてグラフを書けと言われました答えはわかるの Yahoo 知恵袋



1 Y X2乗 2x 3のグラフの頂点を求めなさい 2 Y X Yahoo 知恵袋



2乗に比例する関数 グラフ




Y 3分の1x2乗 2xのグラフの x切片の求め方を教えて下さい Y 0のときの途中 Clear




Y 1 X 2乗 のグラフってどんなんですか 大体でいいので教えてください Clear




例題で学ぶ高校数学 Y Ax2 Q




対数関数のグラフと書き方 数学 理系ラボ



2次関数のグラフ Y X 2



2乗に比例するグラフ 中学から数学だいすき



中学数学 Y Ax 2 のグラフ 中学数学の無料オンライン学習サイトchu Su




3次関数 方程式 のグラフ もう一度やり直しの算数 数学



指数方程式




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ




高校数学 Y Ax 2 Bx Cのグラフ 例題編 映像授業のtry It トライイット
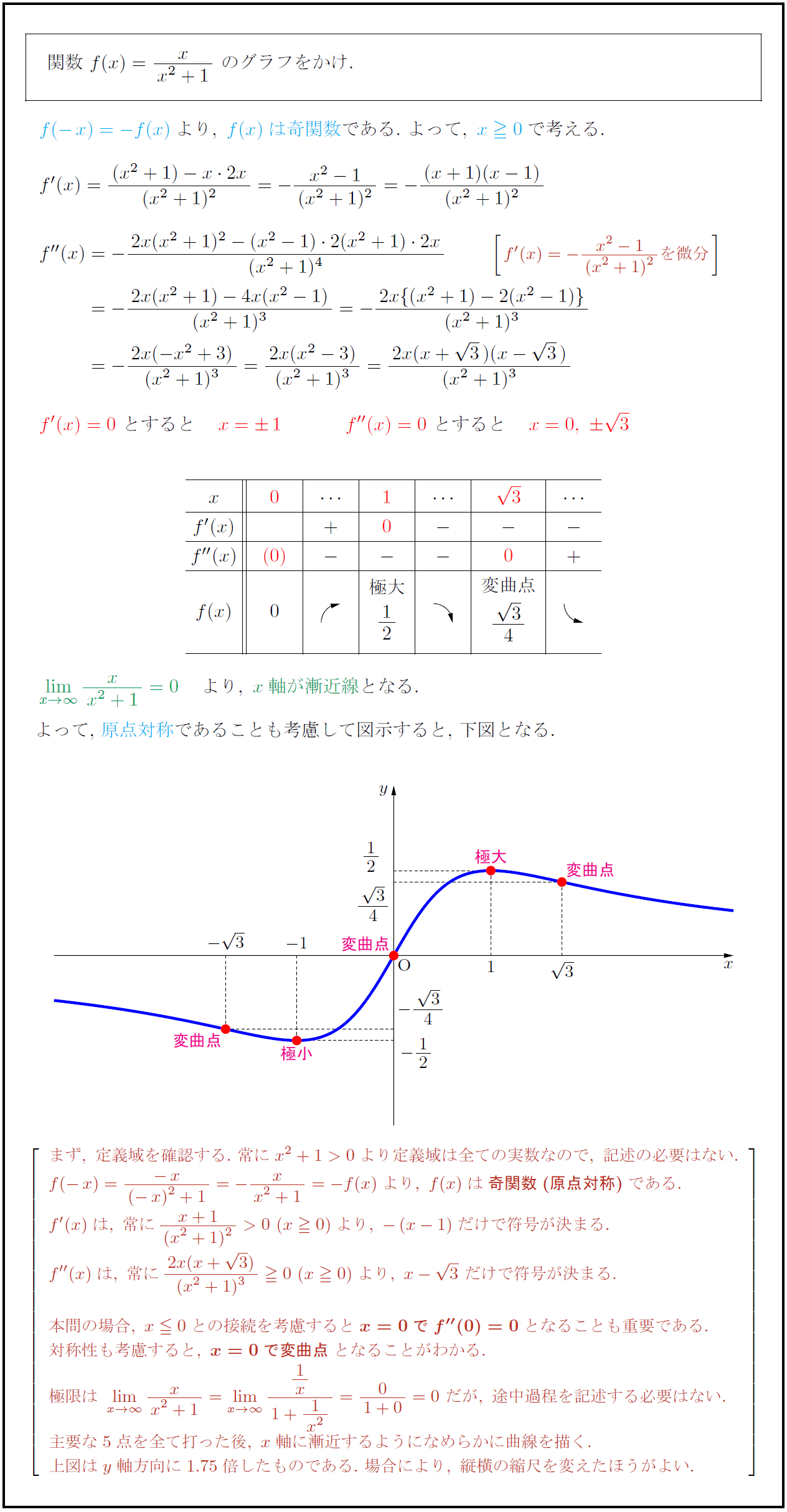



高校数学 分数関数 Y X X 1 のグラフ 受験の月




3年 関数 Y X のグラフ 数学イメージ動画集 大日本図書




Tanのグラフ Y X3乗のグラフ 似てますが どんな関係あるのですか 数学 教えて Goo



2乗に比例する関数 グラフ



2次関数 中学 三角形の面積を二等分する直線の式 勉強ナビゲーター




中3数学 Yはxの2乗に比例 とは 映像授業のtry It トライイット




基本 二次関数y A X P 2のグラフ なかけんの数学ノート



Yx2乗 ニスヌーピー 壁紙



中3 2次関数



Mathematics 関数と証明 大阪府公立 22年前期理数科 働きアリ




絶対値と3乗が付いたグラフの書き方 Y 2 X 1 2x 3 Okwave
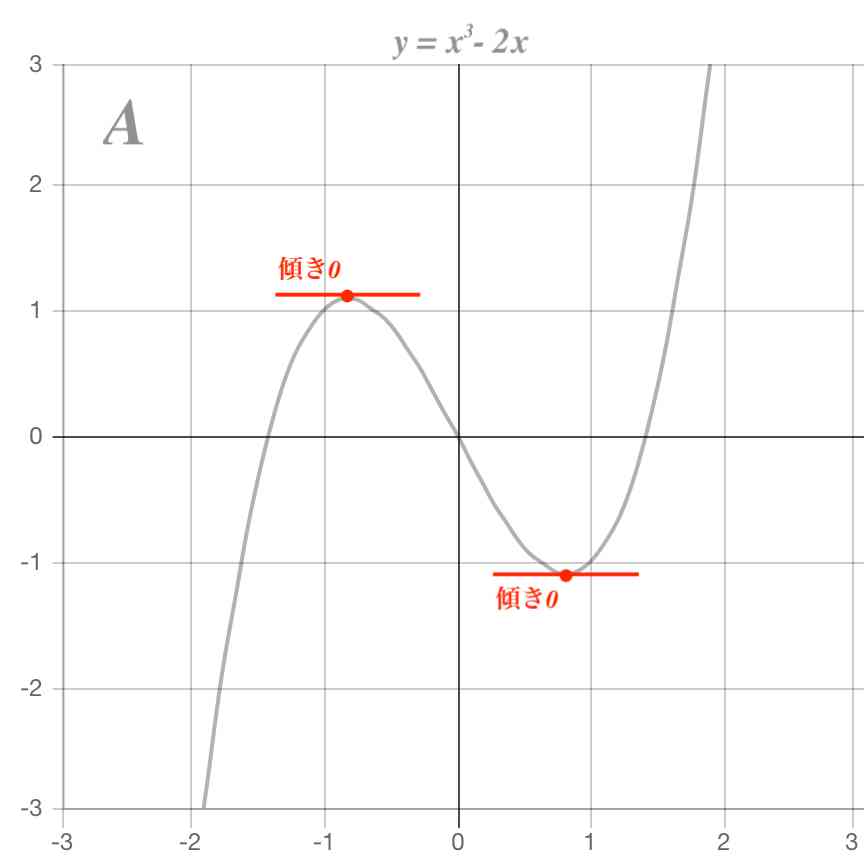



三次関数のグラフの書き方




中学校数学 3年生 数量 2乗に比例する関数 Wikibooks




数学 2次関数 頂点の求め方 オンライン無料塾 ターンナップ



1



Yx2乗 ニスヌーピー 壁紙




この関数のグラフを描きたいのですが 曲線の式は X 2 Y 3 Okwave
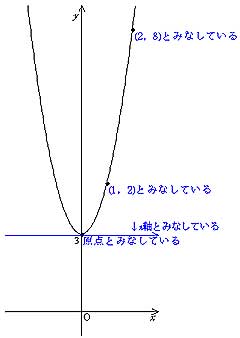



授業実践記録




Y 1 X2乗のグラフ Youtube



F X X2乗 3x 2の解とグラフの答えをお願いいたします 解 って Yahoo 知恵袋




数学 中3 35 二次関数のグラフ Youtube



Y Xの二乗 1 のグラフを書いてくれませんか Yahoo 知恵袋




基本 二次関数y A X P 2のグラフ なかけんの数学ノート




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ




中3数学 Y X2乗のグラフの変域 5分で学習 Youtube




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ




X二乗 y 三乗根 2二乗 二乗 1 恋愛グラフへのボケ ボケて Bokete




数学です Y 1 X 2のグラフで X 2のときは X 2に近づくと無限大に発散す 数学 教えて Goo



二次関数のグラフ



数式のグラフ
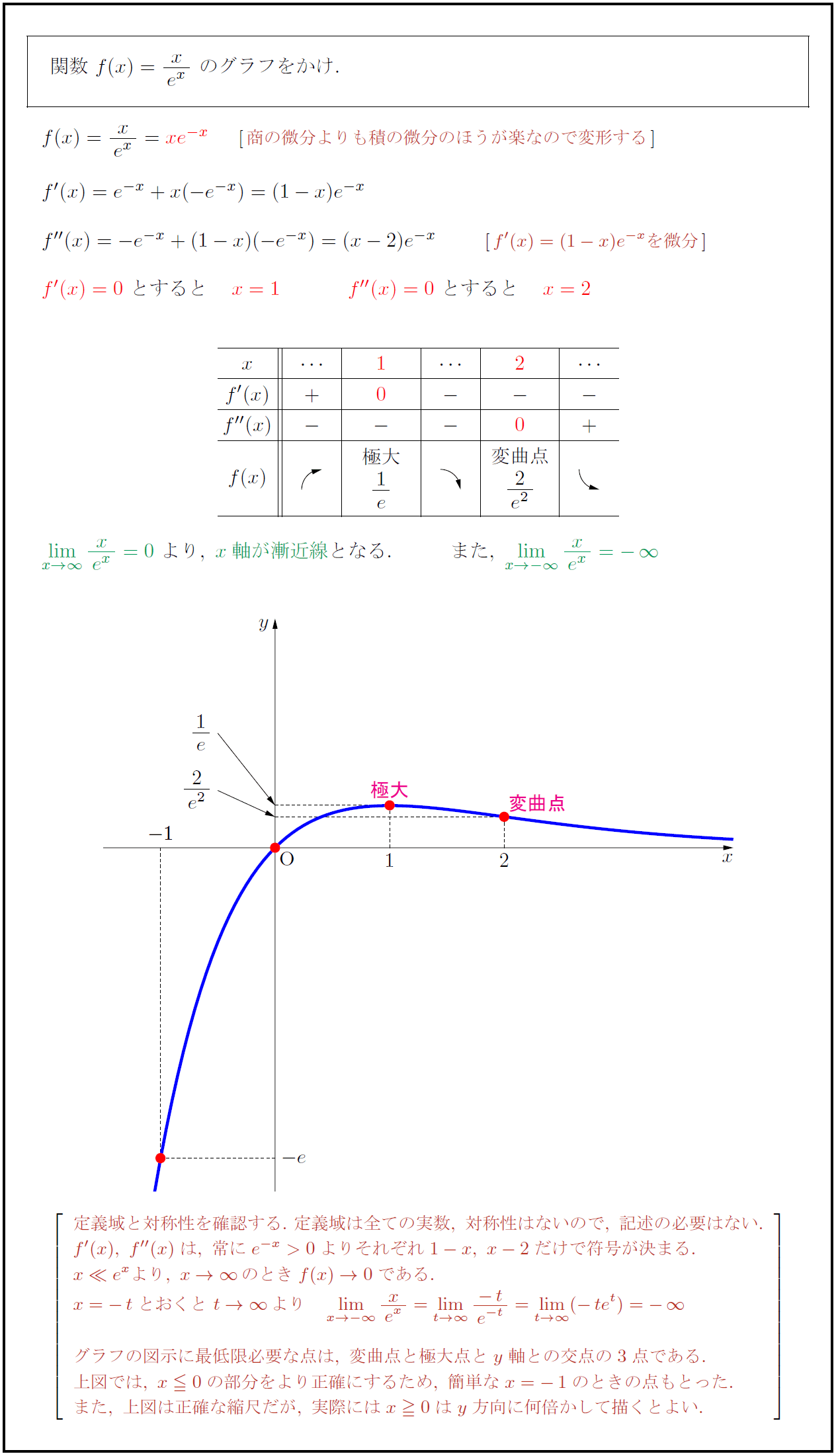



高校数学 指数関数 Y X E X Xe X のグラフ 受験の月




二次関数 Wikipedia




解説がわかりません なぜy x2乗 3xを平行移動した放物線の二次関数はy x2乗 Clear
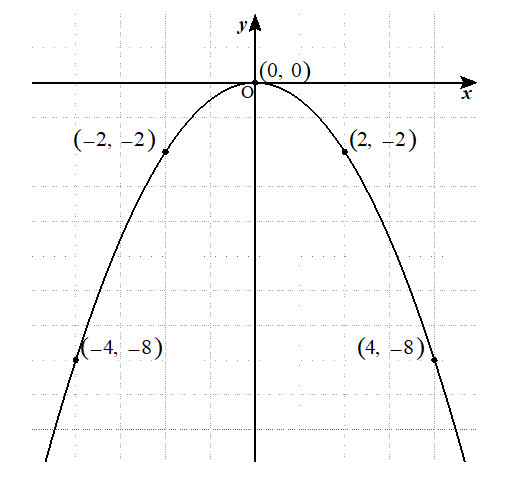



関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ



Y X2乗 4x 1のグラフの書き方を教えてください グラフの画像をつけ Yahoo 知恵袋




数学 二次関数の問題です y 3x二乗 12x c cは定数 1 Okwave




Aは正の定数とする Clear



Y 1 X 2の式のグラフや極限はどのように考えたら良いですか Quora
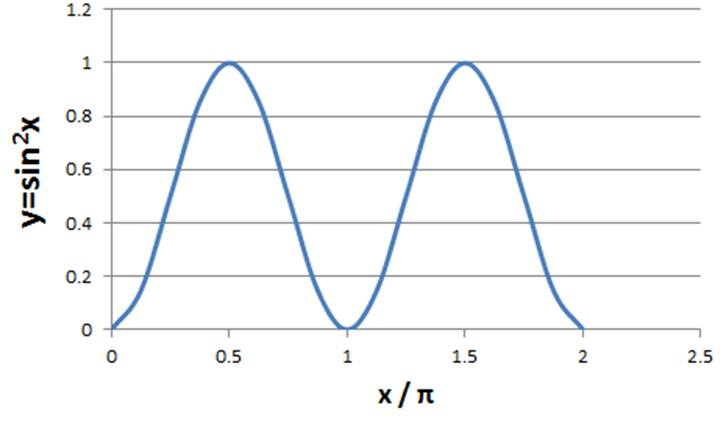



Y Sin 2x のグラフや周期は Y Sin 2 8を微分するとどうなるのか ウルトラフリーダム



関数y X 2のグラフの性質 勉強ナビゲーター
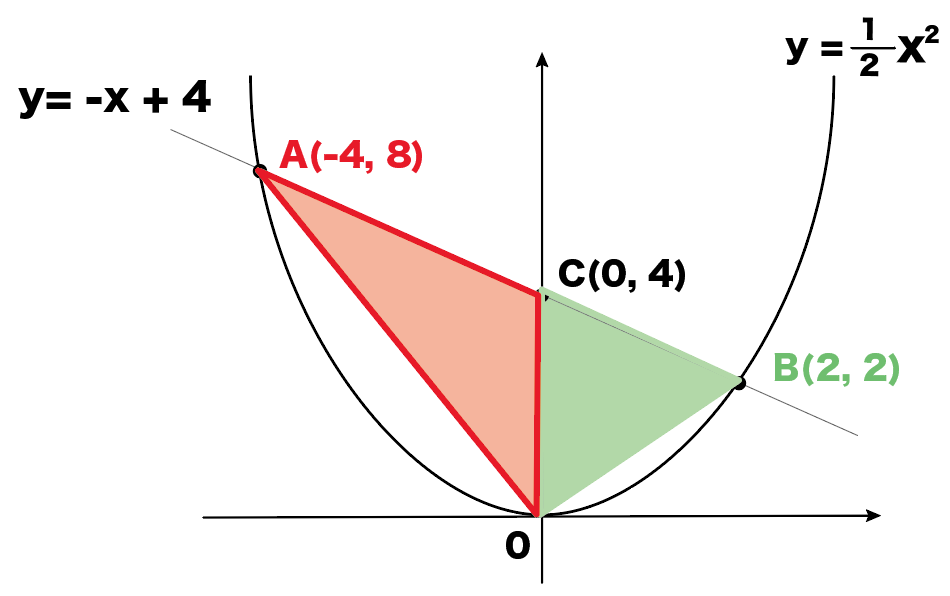



二次関数のグラフで三角形の面積を求める問題の解き方4ステップ Qikeru 学びを楽しくわかりやすく




関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ
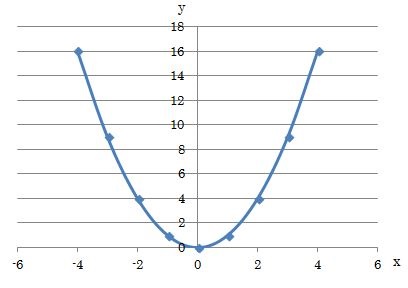



2次関数 方程式 のグラフ もう一度やり直しの算数 数学



1
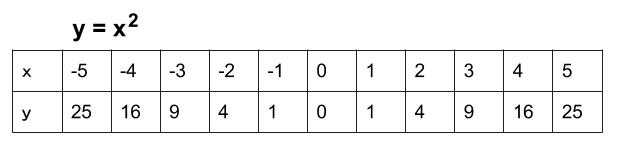



中学数学 Y Ax 2 のグラフ 中学数学の無料オンライン学習サイトchu Su
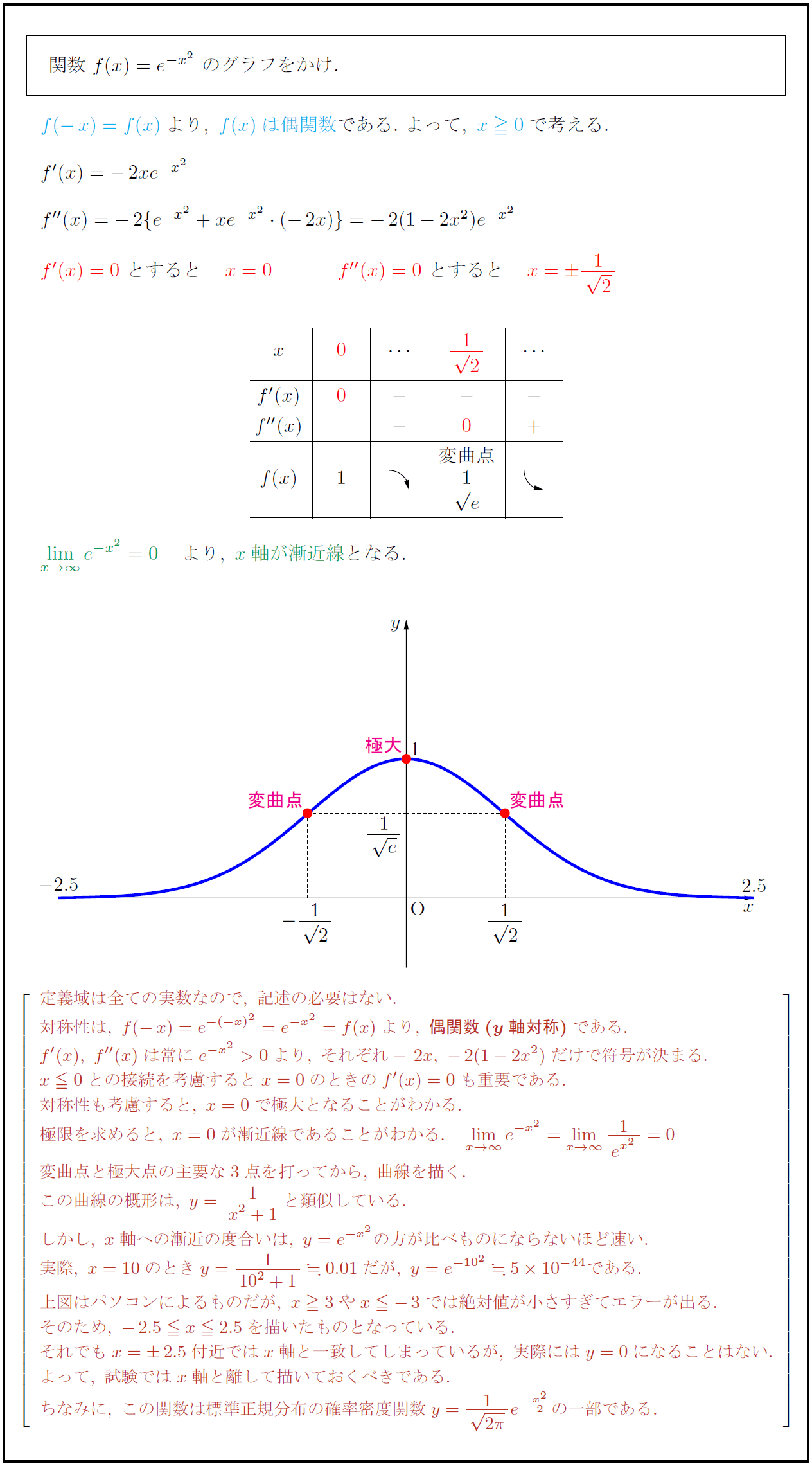



高校数学 指数関数 Y E X のグラフ 正規分布曲線もどき 受験の月




2次関数のグラフ




関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ




中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿