底面積をS、高さをhとすると、 三角錐の体積は、 1/3 Sh になるんだ。 つまり、 (底面積)×(高さ)÷ 3 ってわけだね。 今日は、この公式で体積を計算してみよう!! 使って覚えるのが一番だからね。 三角錐の体積の求め方がわかる3ステップ
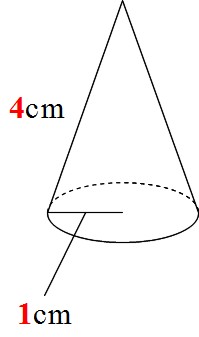
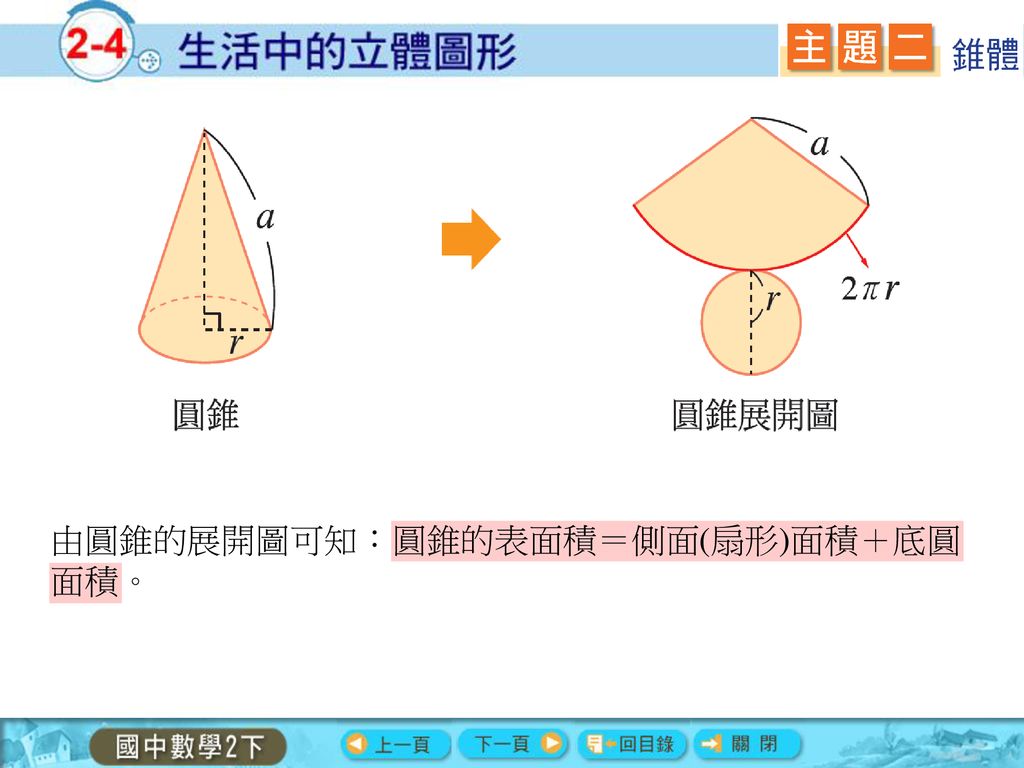
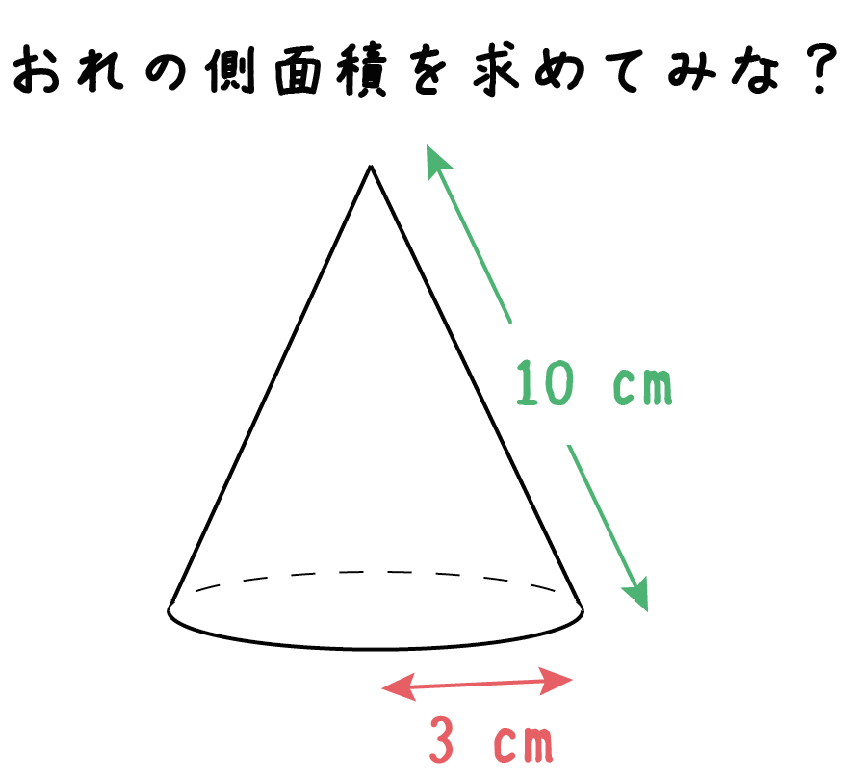
三角錐 側面 面積- 側面積= LRπ 例題: 底面の半径が1cm、母線の長さが4cmの円錐の表面積を求めよ。 (解答) 表面積=底面積側面積です。 底面積は円だから半径×半径×πより、 底面積=1×1×π=π 側面積は母線×半径×πで求められるから、 側面積=4×1×π=4π よって、表面積は π4π=5π底辺の1辺の長さaが2、高さhが3の正四角錐の体積・表面積・斜辺の長さ 体積 V:4 側面積 S 1 : 表面積 S 2 : 斜辺の長さ b:
三角錐 側面 面積のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 | ||
 |  |  |
 | ||
「三角錐 側面 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「三角錐 側面 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「三角錐 側面 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 | ||
 | ||
「三角錐 側面 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
 |  | |
「三角錐 側面 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
 |  |  |
「三角錐 側面 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  |  |
「三角錐 側面 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 | ||
「三角錐 側面 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |
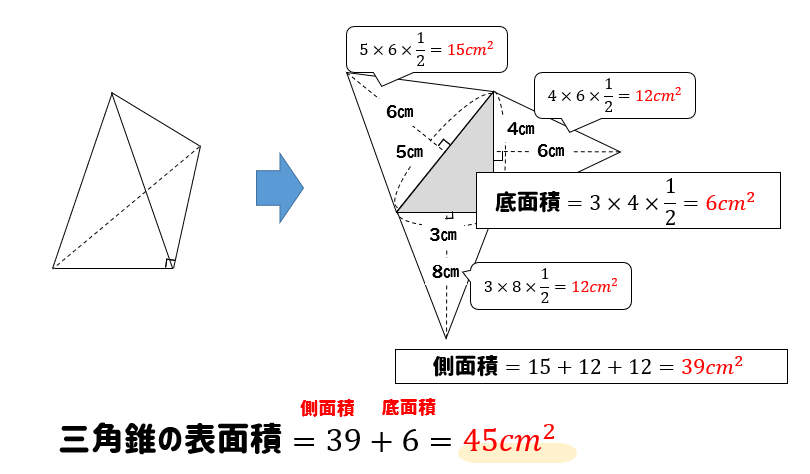
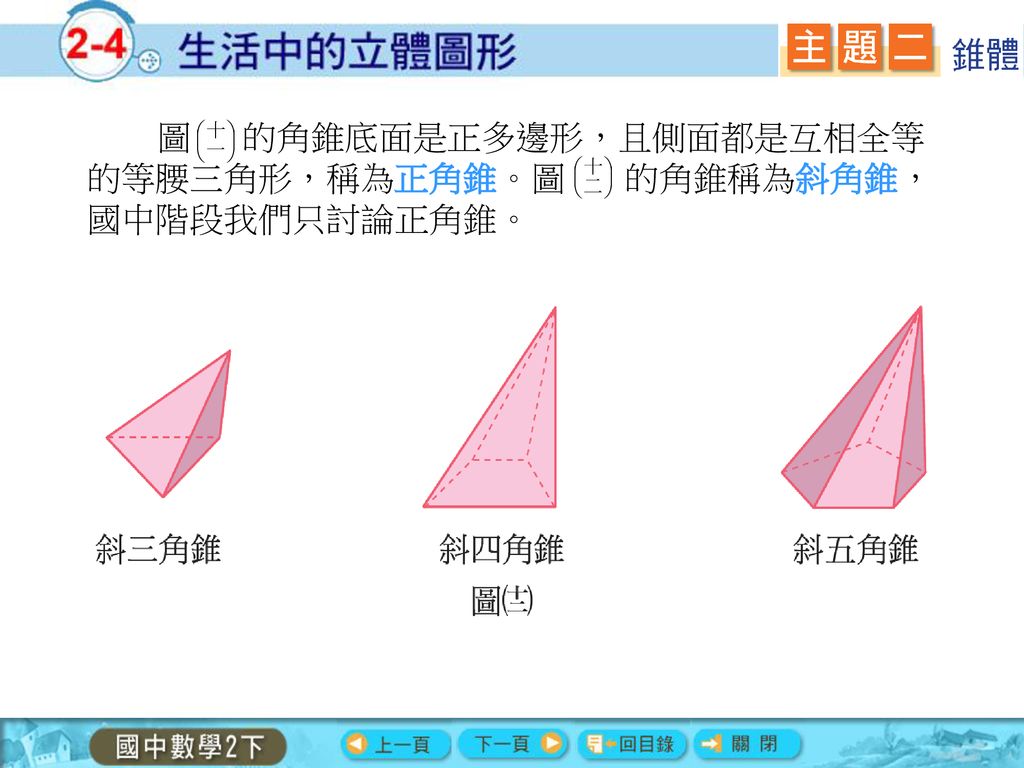
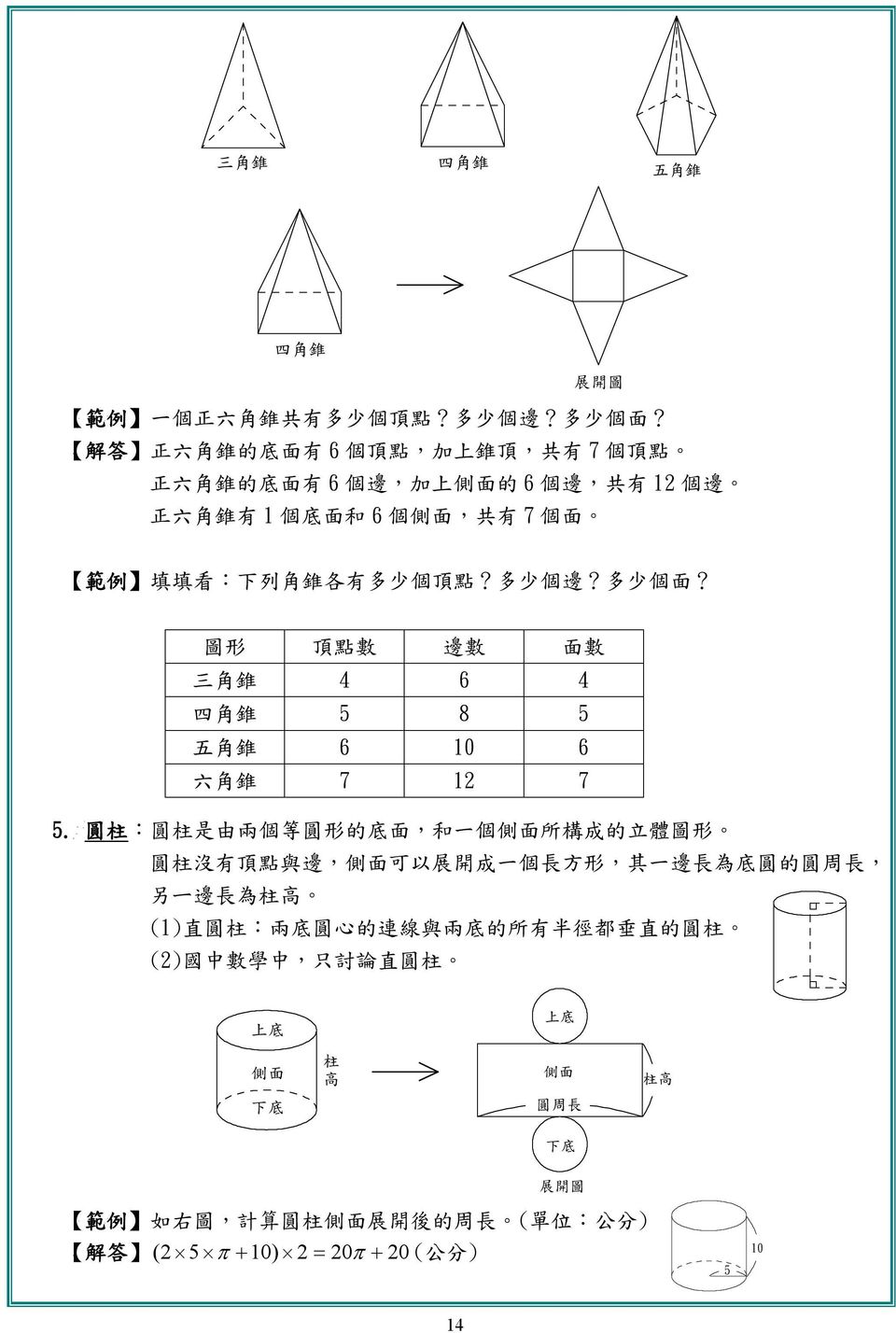
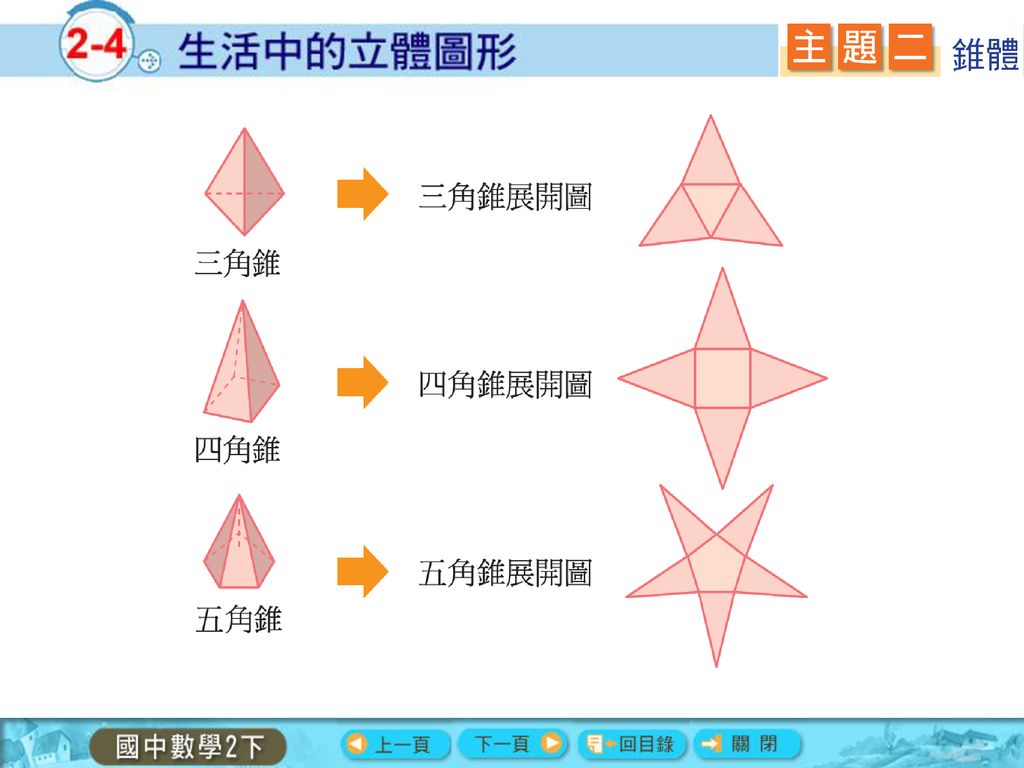
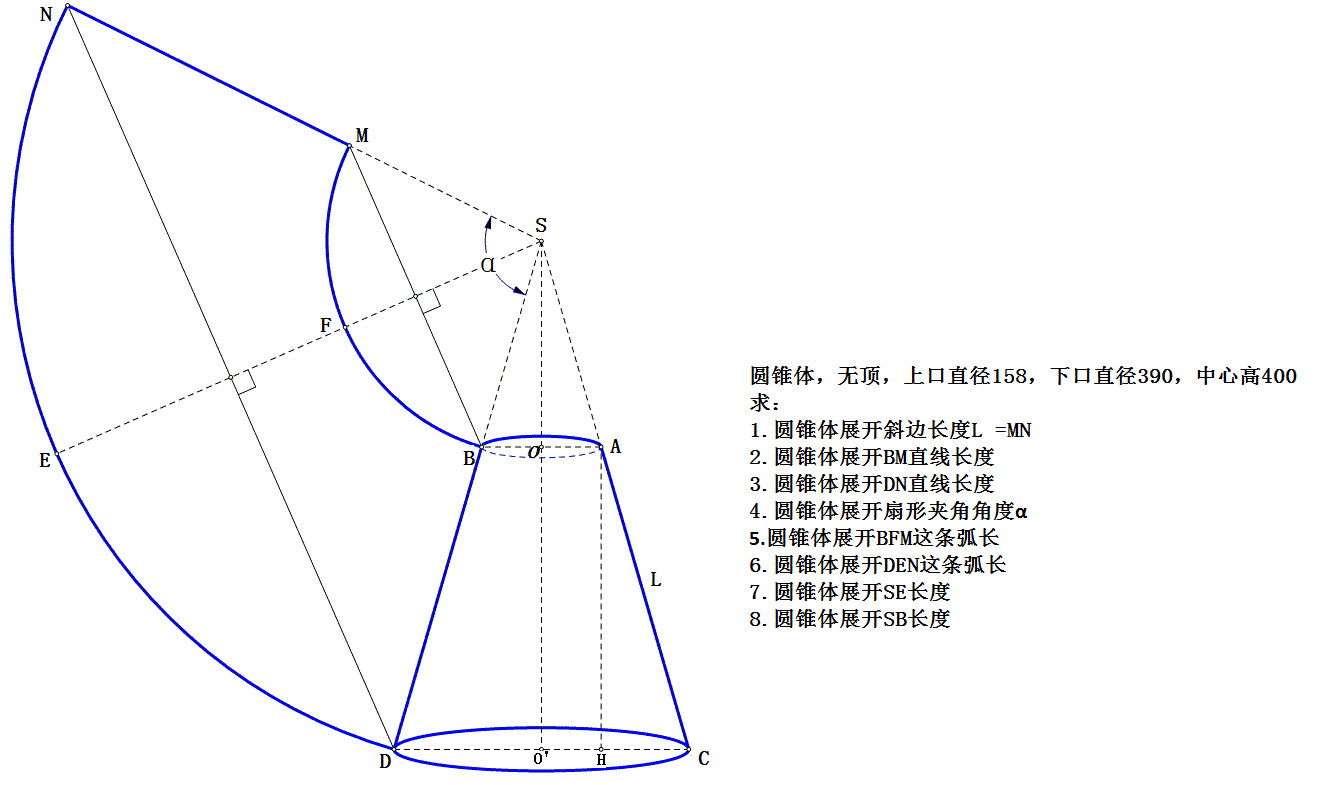
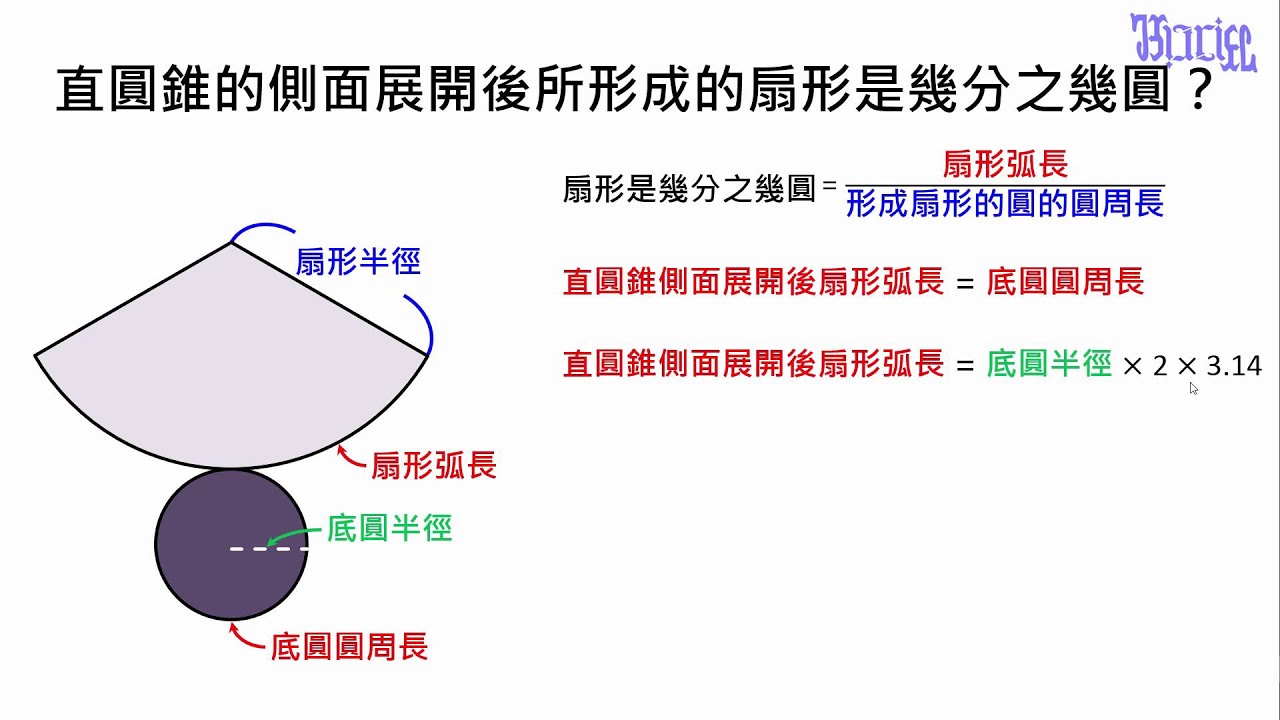
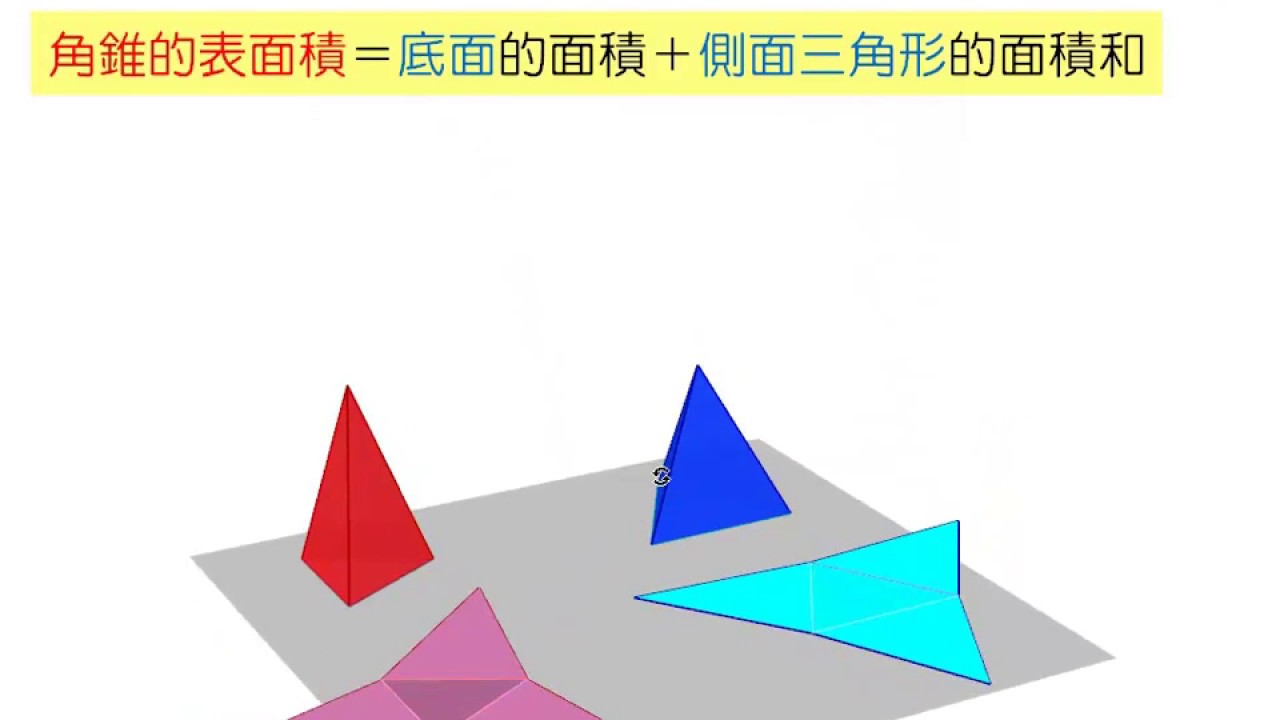
側面のおうぎ形の中心角の大きさ=底面の半径×360÷母線 側面の面積=底面の半径×母線×円周率 (例題2) 上の図は、底面の半径が9cmの円錐から、上の部分を切り取ったものです。 この図形の表面積は何cm²でしょう。 まずはこの図形の展開図を書いてみ底面の三角形に対して、側面の三角形が3つ分くっついている形 になります。 つまり、四角錐の表面積とは次のように求めることができます。 三角錐の表面積=底面積 側面積(三角形 つ分) では、実際に問題を解いてみましょう。 次の三角錐の表面積
Incoming Term: 三角錐 側面 面積,




0 件のコメント:
コメントを投稿