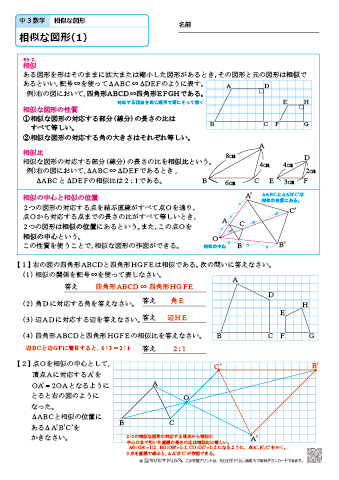
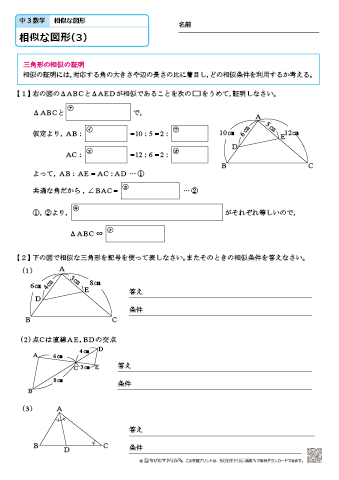
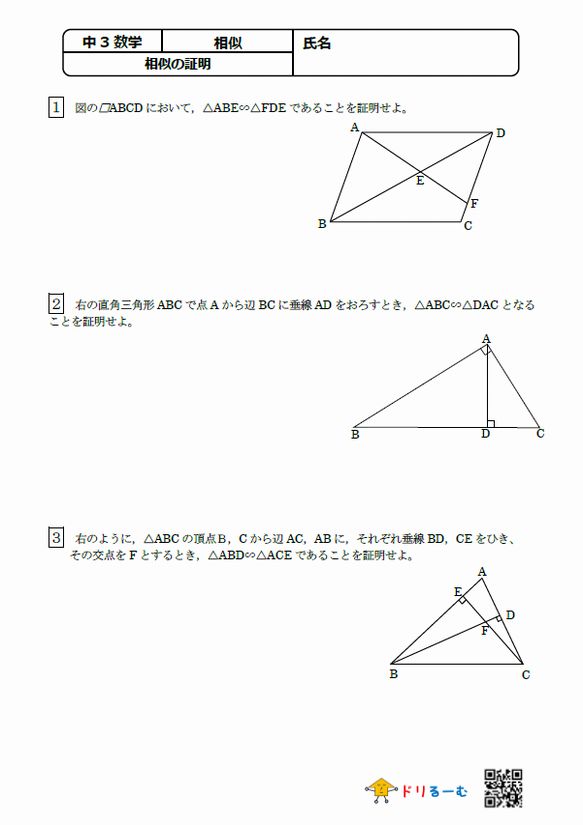
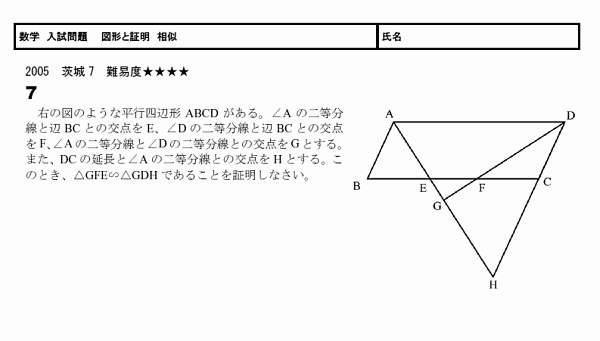
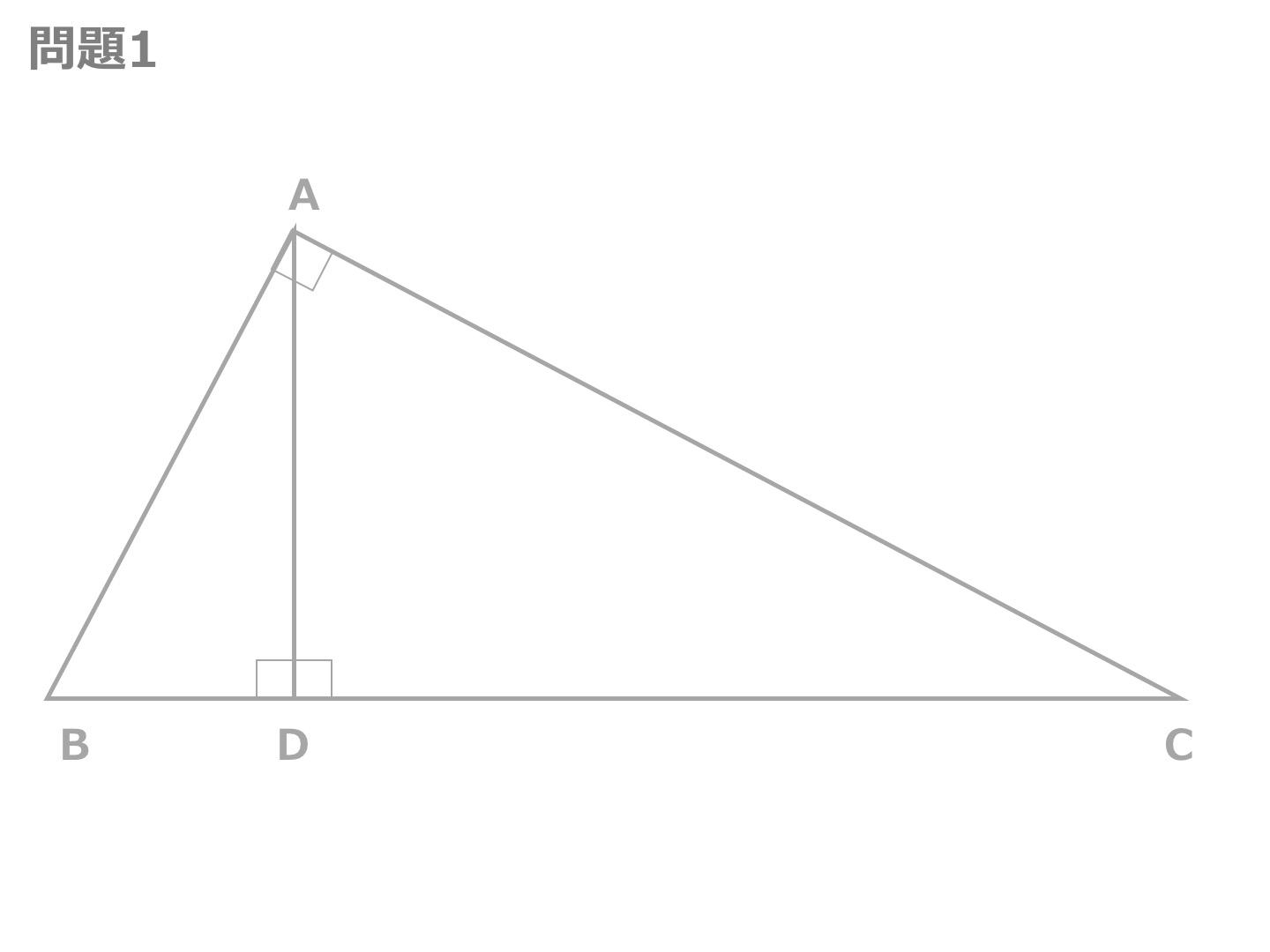
相似な図形の証明問題です。 入試でもよく出題されるので、いろいろな問題を解くようにして見てください。 ポイント 図の中で証明する三角形に印をつけて、相似条件に当てはまるかを考えてみてください。 すぐに解けない場合は、解答・ 角形を見つけ、証明の仕方を知る。 三角形の相似条件を適 の相似条件を確認してから、証明問題に取り組む 言葉や式を使って表して 6 切に使って、説明を書 ようにする。 いる。 相似な三角形を見つけて、その根 くことができる。数学35章図形と相似「相似な図形」<準備問題②> 組 番 名前 1次のχの値を求めなさい。 (1)2:5=χ:15 (2)χ:2=5:4 (3)χ:2=3:5 (4)χ:5=(χ-6):3 線分AD上に点Pをとると, となります。 これを次のように証明しました。 をうめて

相似の証明 チーム エン
相似の証明 練習問題
相似の証明 練習問題-→ 相似の証明できない 2組の比が解っている「間の角」∠apqで同様に行うと ∠apq = ∠abc が言えない (↑pq//bcという前提がないので同位角が等しいと言えない) → 相似と証明できない (証明2) apq∽ crqは 型同様、okA^2b^2=c^2 a2 b2 = c2 英語ですが,三平方の定理の証明を105個解説しているすさまじいサイトがあります。 →Pythagorean Theorem 105個の中で,個人的に「簡単で美しい」と思った証明を4つ(#3,6,42,47)ほど紹介します。 目次 正方形を用いた証明 相似を用いた



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス
相似であることを証明するこ とができる。 三角形の相似 条件を用いた 証明の進め方 を理解してい る。(練習問題 の解決状況の 分析) 7 2.2つの三角形が相似である ことを、使う相似条件の見通し をもって証明することができ る。 見出した図形の ∽ を証明すれば相似の比を使えます。 証明しましょう。 線分の情報がありますが、対応する線分の比を1組しか作れないですね。 そのため「2組の角がそれぞれ等しい」で攻めていきます。 まず共通している角なので、こんにちは、ウチダです。 今日は、中学3年生で習う 「三角形の相似条件」 について、まずは図形の相似を解説し、次に三角形の相似条件が $3$ つである理由を明らかにしていきます。 また記事の後半では、狙われやすい証明問題をいくつか用意しましたので、ぜひチャレンジしてみて下さい。
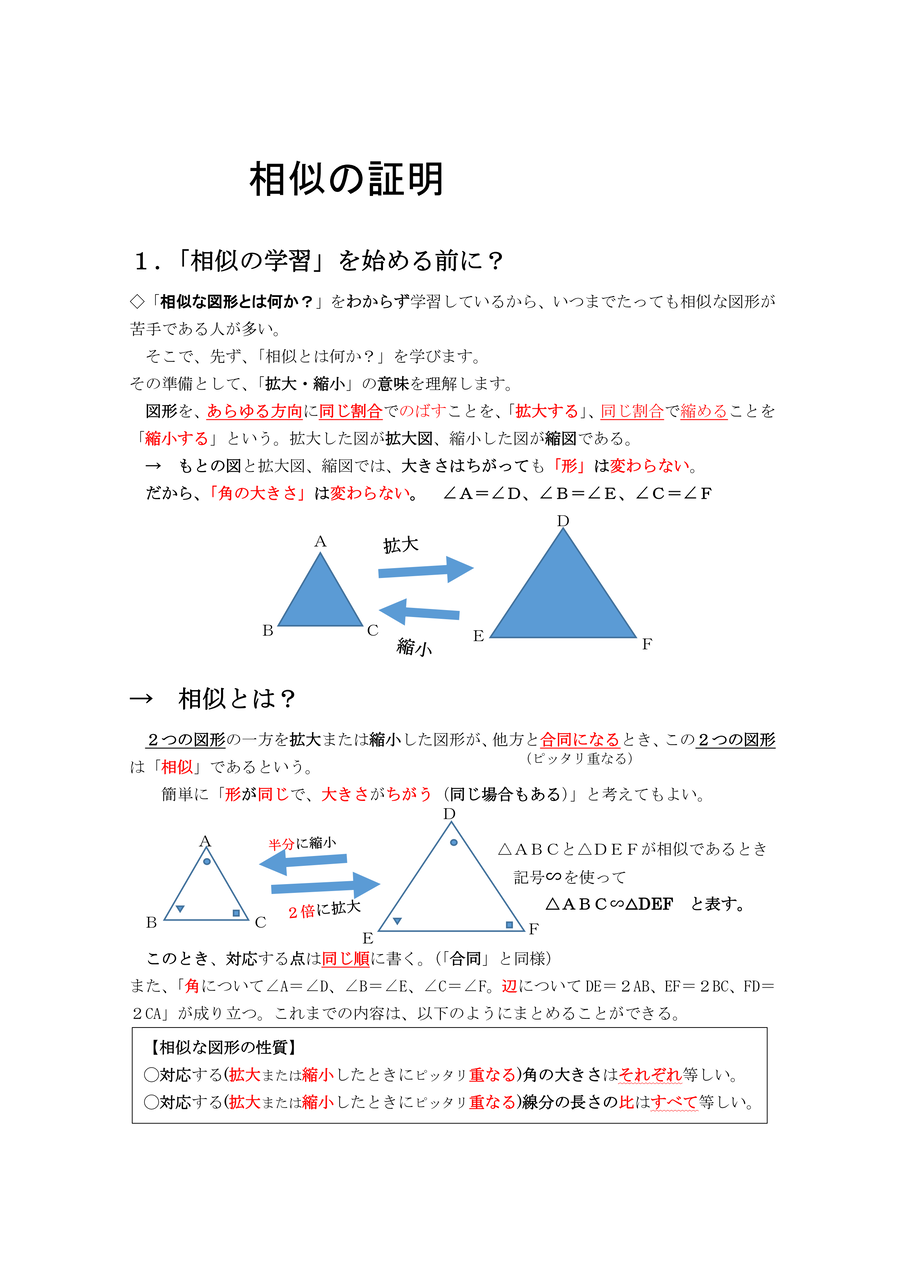
『相似な図形』の単元の中から 平行線と線分の比という内容について解説してきます。 ここでは、相似な図形の性質をつかって いろんな図形の辺の長さを求めていきます。 長々と解説をするよりも 問題を見ながら、実践を通して学習するのが良いので22 学校数学における相似の定義と相似な図形の性質 小学校6 年生では,中学校で学習する素地として,拡大と縮小を学習する.小学校の教 科書では,いろいろな縦と横の比の図を見せ,形が同じで大きさが違う図形について考え相似な図形/三角形の相似条件/相似の証明:2 辺の比とその間の角/2 組の角が等しい/ 直角三角形など /三角形の相似と長さ/FdData 中間期末製品版のご案内
(証明) となるので と の固有値は等しい. 定義 5 35 (相似) 正方行列 , に対して をみたすある正則行列 が存在するとき, と とは 相似(similar) または 同値(equivalent) であるという.証明 (合同・相似)が苦手な人へ 教遊者 IC Channel 192K subscribers Subscribe 中2,中3,受験生平行と合同,三角形と四角形,相似「証明 (合同・相似)が苦手な人へ90%以上の証明に使えるテンプレートと素材まとめ」デジタル板書データ Watch later 相似変換は固有値を保存する † 相似変換によって固有値が変化しない すなわち 相似な行列というのは、固有値が等しい行列のこと これでようやく「どこが似ているか」が分かった! ← 相似 = 「相手と似ていること」 証明:



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




数学 中3 48 相似の証明チャレンジ Lv 3 Youtube
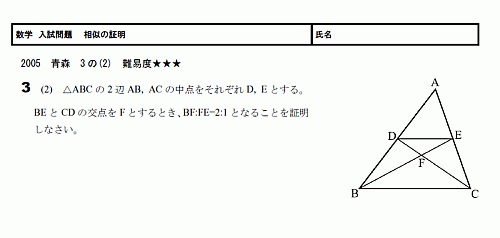
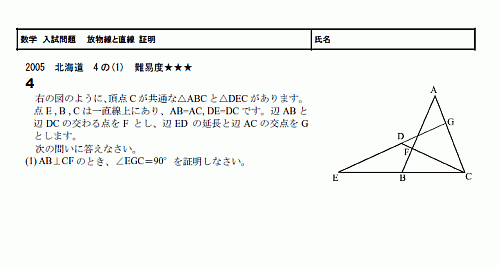
数学 高校入試問題 相似の証明 05青森県3の(2) 難易度★★★(pdf) 相似の証明の問題。 中点連結定理を利用します。 難易度は3にしていますが、2でもいいかもしれません。 ちょっと驚いたこと。相似の証明2 おろし、交点をD, Eとする。 このとき ADB∽ BECを証明しなさい。 2 ABCの頂点B, Cからそれぞれ辺AC, ABに垂線を引き、交点をそれぞれD, Eとする。 (1) ABD∽ ACEを証明せよ。 (2) AB=9cm, AC=8cm, DがACの中点のときAEの長さを求めよ。 3円周角と図形の証明 円周角の定理の逆 円周角の定理の活用 7 三平方の定理 三平方の定理の証明(1) 問題一括 (3,793Kb) 解答一括 (4,569Kb) 三平方の定理の証明(2) 三平方の定理の証明(3) 三平方の定理(1) 三平方の定理(2) 三平方の定理の逆 平面図形での活用(1)



相似の証明問題でマスターしておきたい3つのパターン Qikeru 学びを楽しくわかりやすく



中学数学 三角形の相似条件 中学数学の無料オンライン学習サイトchu Su
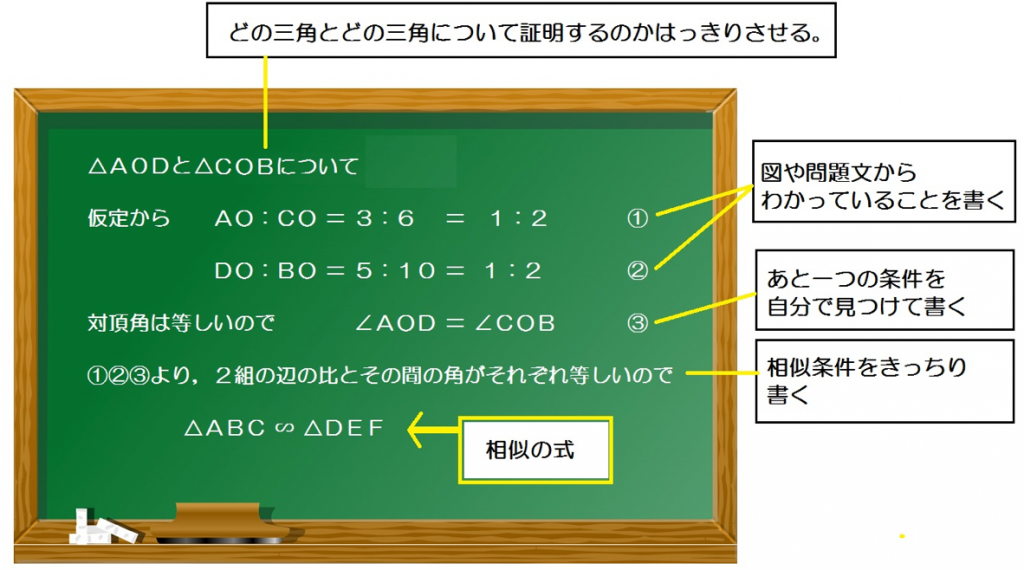
証明したいことを図(自作)に印づける。 問題文から証明に使えそうなヒントを図に書き入れる。 合同条件(または相似条件)の3つからどれが当てはまるかを探る。 条件が揃わない場合は、 図から判断して条件に当てはまりそうなところが無いかを探る。動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru これこそが、図形問題なのである。 測ったらタルトが本当に45度で切られていて見事だった 肩慣らしとして、これを解いてみよう。 出題は、「xの角度を求めよ」。 三角形の内角の和は180度。 かつタルトは二等辺三角形なので、角ABCは (180度45度)/2 = 675




無料 中3数学 標準問題 解答プリント 327 図形の相似2 相似条件と証明




三角形の相似の証明の解き方 2 現役塾講師のわかりやすい中学数学の解き方
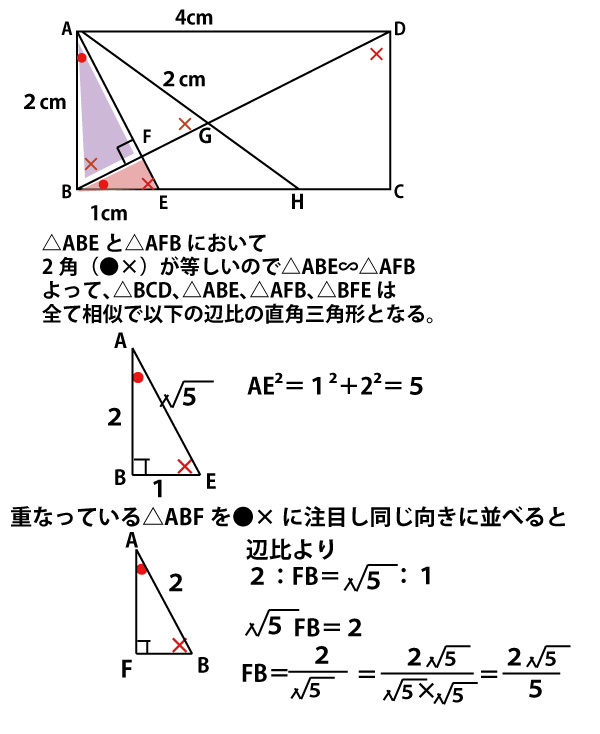
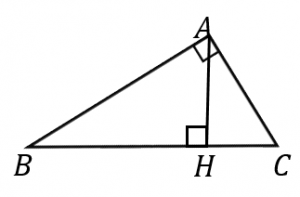
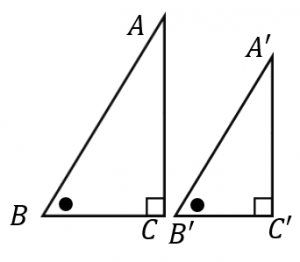
三角形の相似の証明 中学2年で学習した、三角形の合同の証明とほぼ同じです。 用いるのが合同条件ではなくて、相似条件になっただけです。 三角形の合同の証明があやふやな人は、そこから学習をしましょう。 急がば回れです。 証明相似の証明・長さ 2 組の辺の比とその間の角 問題 右の図のように,ab=9,ac=12 の abc が ある。点d が辺ab上に,点eが辺ac上にあり, ad=8,ae=6 となっている。このとき, abc∽ aed であることを証明せよ。 (岩手県)(**) 解答欄相似比と面積比,体積比の公式の証明 レベル ★ 基礎 平面図形 更新日時 相似な平面図形について,面積比=相似比の二乗 相似な空間図形について,体積比=相似比の三乗 面積比をきちんと理解できれば体積比もほぼ同様に理解できるので




証明 合同 相似 が苦手な人へ 教遊者



本時のねらい 図形の中から相似な三角形を見出し 相似条件を用いて証明することができる Ppt Download
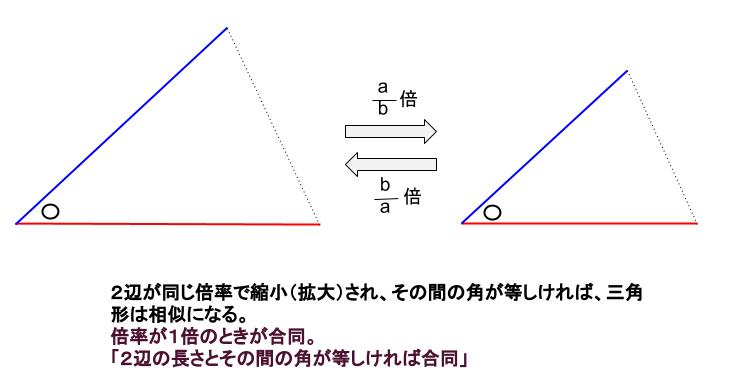
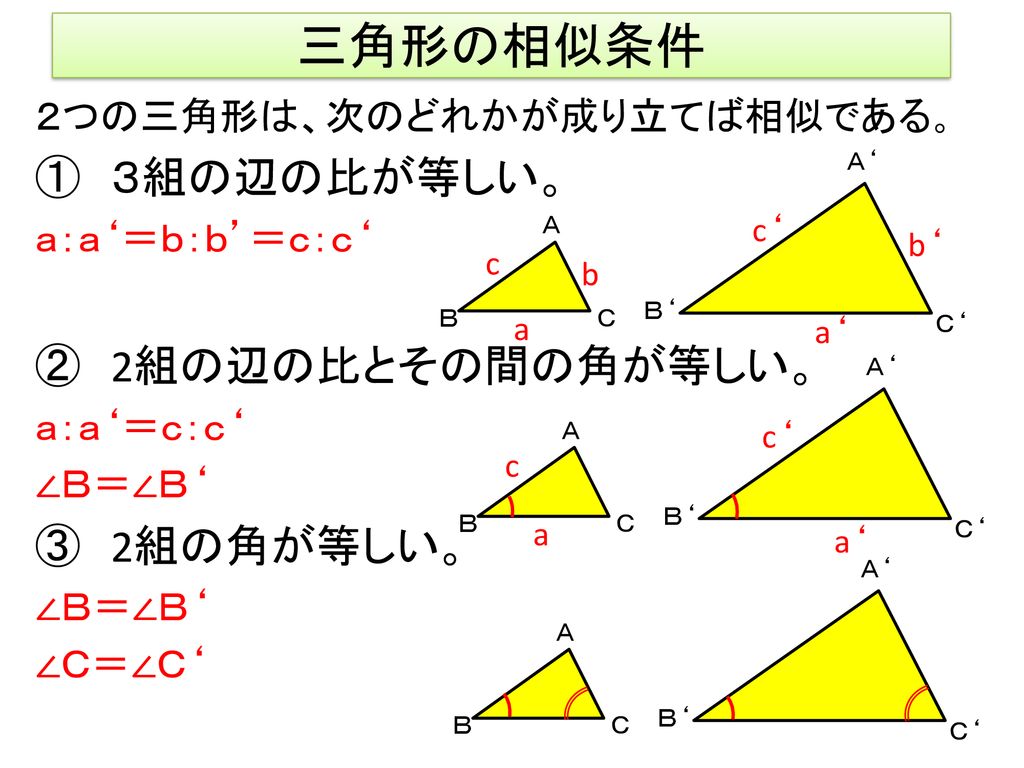
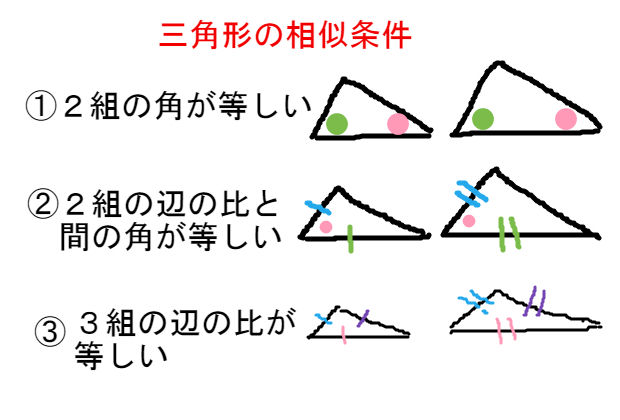
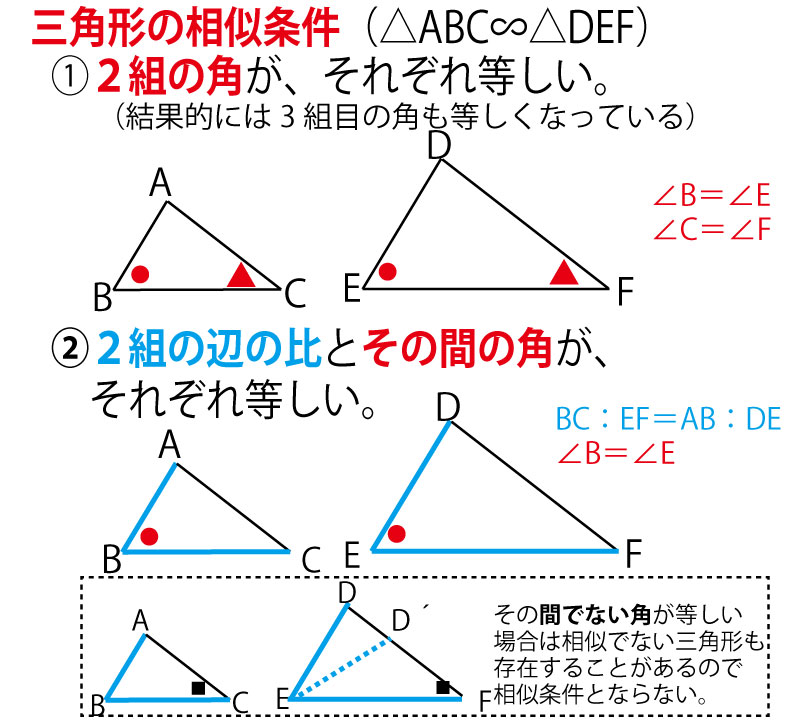
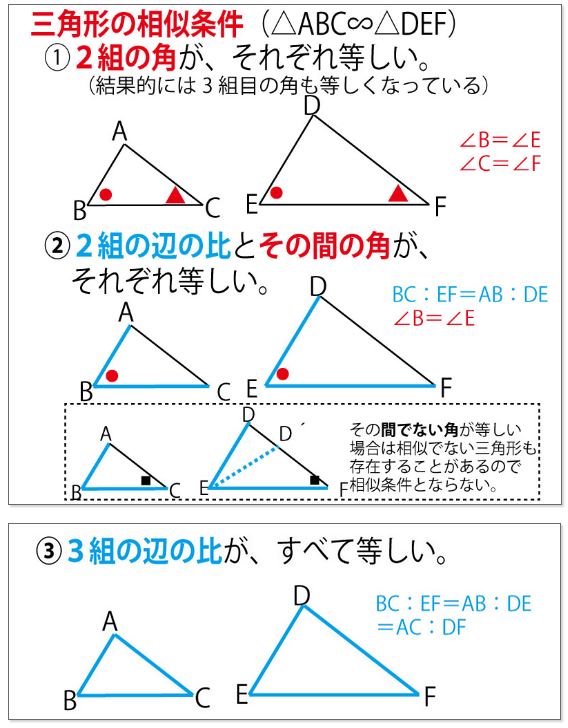
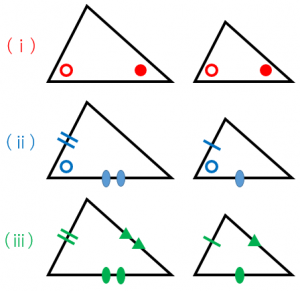
一方証明問題では、記述によって2つの三角形が合同であることや相似であることなどを説明します。よって 数ある単元の中でも図形の証明は、異質な単元 であると言えるでしょう。 独特であるということがすなわち証明問題が難しく感じられる理由 です。相似であることを証明するには「2組」を示せば十分だということ 右図では ∠B=∠Q, ∠C=∠R を示せば, ∠A=∠P は自動的に成り立つ. (2) 「3組の辺の比がそれぞれ等しい」という書き方は2種類ある.相似とは ある図形を拡大、縮小した図形は、もとの図形と相似であるといいます。 相似な図形どうしは、まったく同じ形をしているといえます。 例えば下の図の四角形 \(abcd\) と四角形 \(hefg\) は相似



図形と証明 相似 スタディーx




中3数学 円と相似 の証明問題の解き方のコツ 映像授業のtry It トライイット
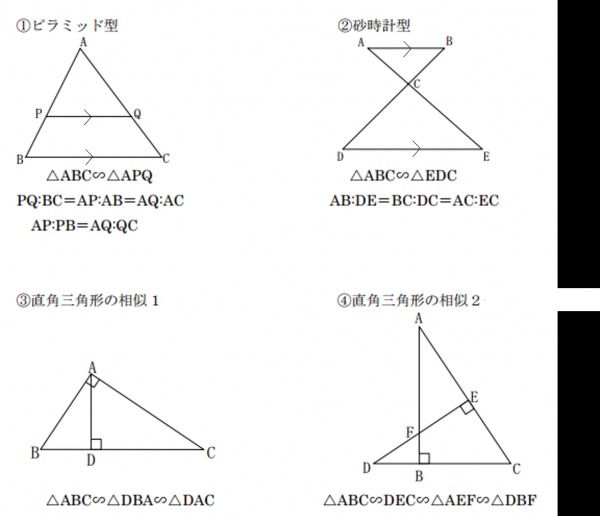
定理の証明 ① abcと adeにおいて de//bcより、平行線の同位角は等しいので ∠abc=∠ade, ∠acb=∠aed よって2組の角がそれぞれ等しいので abc∽ ade 相似な三角形の対応する辺の比は等しいので adab=aeac=debc ② f eを通りabと平行な直線をひき、bcとの交点をfとする。これは相似条件を満たすという流れで示していきます! 円周角について adeと bceの角であることを示すために書き換えると、 ∠cad=∠ead ∠dbc=∠ebc より、 ∠ead=∠ebc ① 角を共有しているので、 ∠dea=∠ceb ② ①、②より相似条件を満たしているので、
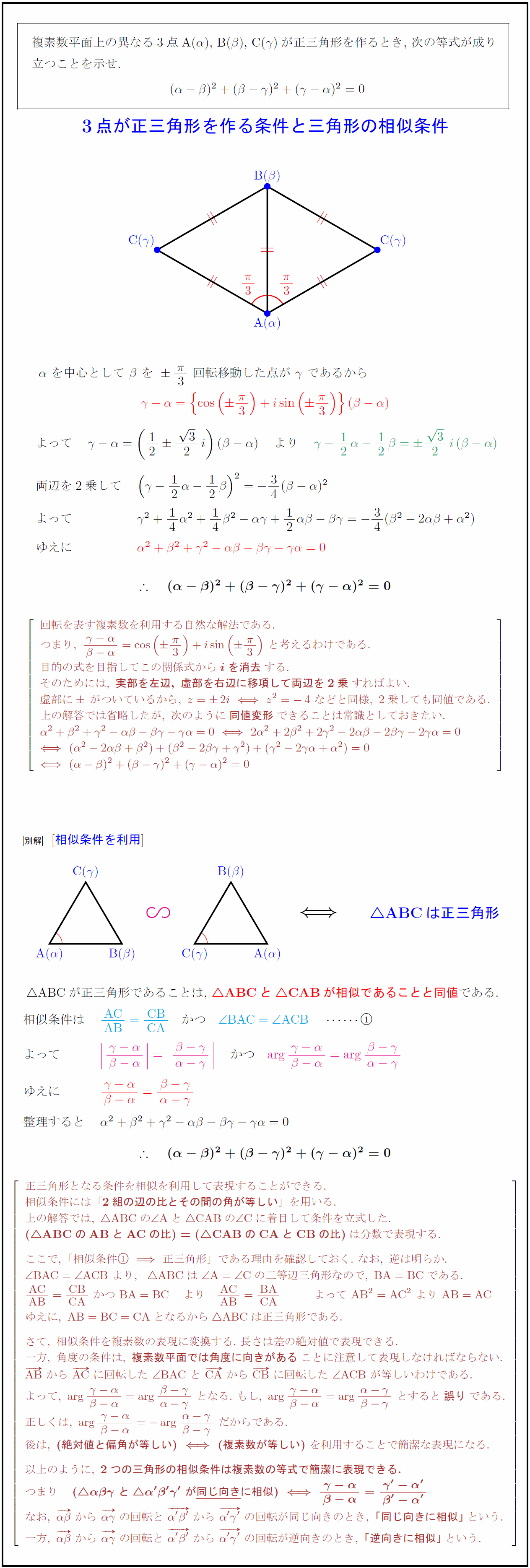



高校数学 複素数平面上で3点が正三角形を作る条件と三角形の相似条件 受験の月




三角形の相似条件 証明の練習になる簡単な問題を紹介 中学や高校の数学の計算問題
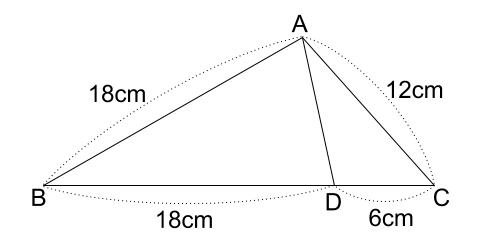



中学数学 相似の証明 その1 中学数学の無料オンライン学習サイトchu Su



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス



相似の証明の順番について教えてください この画像の問題な Yahoo 知恵袋




相似な図形 補助線を引いて考える相似の問題 中学生からの勉強質問 数学 進研ゼミ中学講座



中学数学 相似の証明について質問です Abc Adeは正 Yahoo 知恵袋
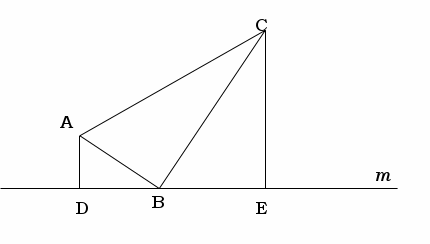



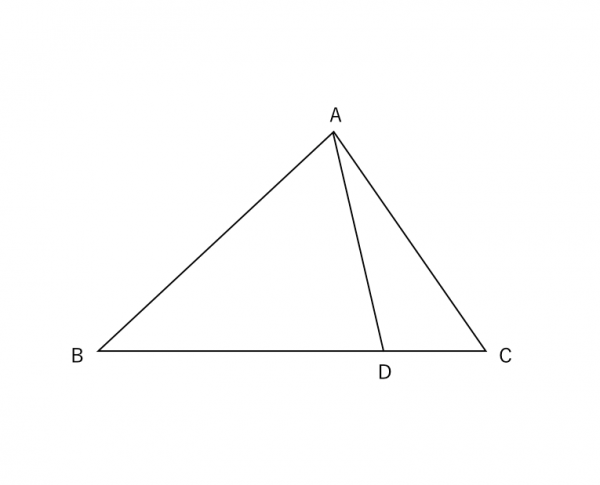
相似の証明2



相似の証明 2つの正三角形と共通な角 勉強ナビゲーター




都立入試 数学 図形の証明問題 大問4問2 図形の相似のひみつ 都立高校入試で成功する方法



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



14年前期 千葉県公立高校入試 数学 第4問 図形の証明 配点15点 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




相似条件とは 三角形の相似条件はなぜ3つなの 証明問題アリ 遊ぶ数学



中3数学 いろいろな相似の証明の特訓練習問題 Atstudier



1




5章1節2 三角形の相似条件2 数学のすすめ



相似条件を上手く利用するポイント 苦手な数学を簡単に
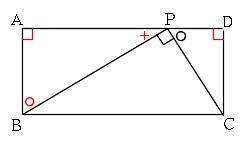



Mathematics 相似 2 相似の証明 やさしい入試問題を使って 働きアリ
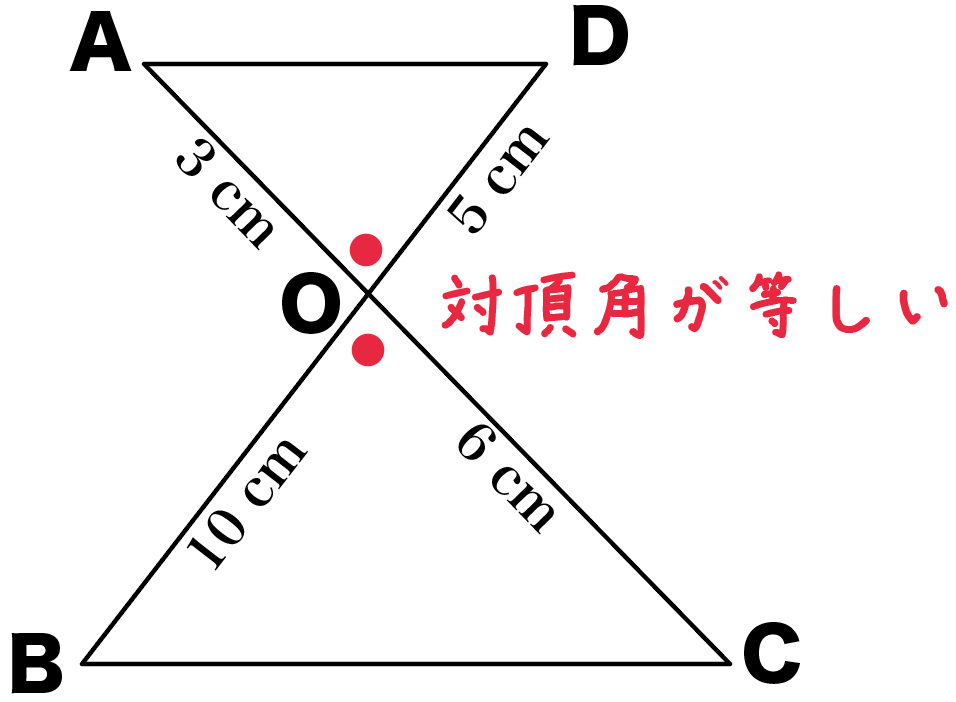



相似の証明問題でマスターしておきたい3つのパターン Qikeru 学びを楽しくわかりやすく



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス
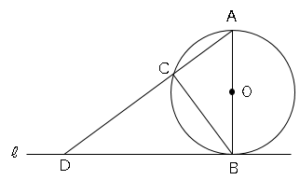



円が2つある相似の証明問題と面積を求める問題 数学の要点まとめ 練習問題一覧




中3数学 図形と相似5 相似条件と証明 平行であることの証明 すべて無料 星組の中学数学講座




無料 中3数学 基本解説 解答プリント 327 図形の相似2 相似条件と証明
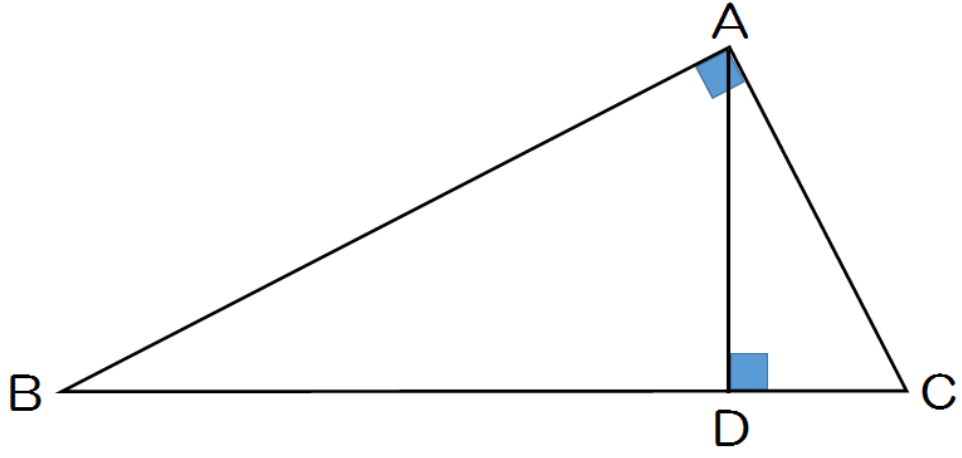



相似の証明問題でマスターしておきたい3つのパターン Qikeru 学びを楽しくわかりやすく




中3 数学 6 3 相似の証明 円 Youtube



合同と相似の複合問題 制限3分 中学数学 理科 寺子屋塾の復習サイト




相似の証明10 Geogebra




相似の証明3 チーム エン



三角形の相似 合同条件 優技録



数学の相似証明問題です この問題の答えと解説を教えて下さい Yahoo 知恵袋



高校入試 英語 数学 図形と相似 三角形の相似証明




三角形の相似条件



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典




相似の証明01 Geogebra



Studydoctor三角形の相似条件 中3数学 Studydoctor




数学 中3 46 相似の証明チャレンジ Lv 1 Youtube




中学3年 数学 東京書籍 新しい数学 相似な図形 平行線と比 赤城 ᐡᐤᐡ




三角形の相似条件と基本的な証明 無料で使える中学学習プリント




中3 相似証明問題 この下のような証明問題の場合どことどこの図形でやるか Okwave




平行線と相似 証明 Youtube



1



図形と証明 相似 スタディーx



Studydoctor折り返し長方形と相似の証明 中3数学 Studydoctor
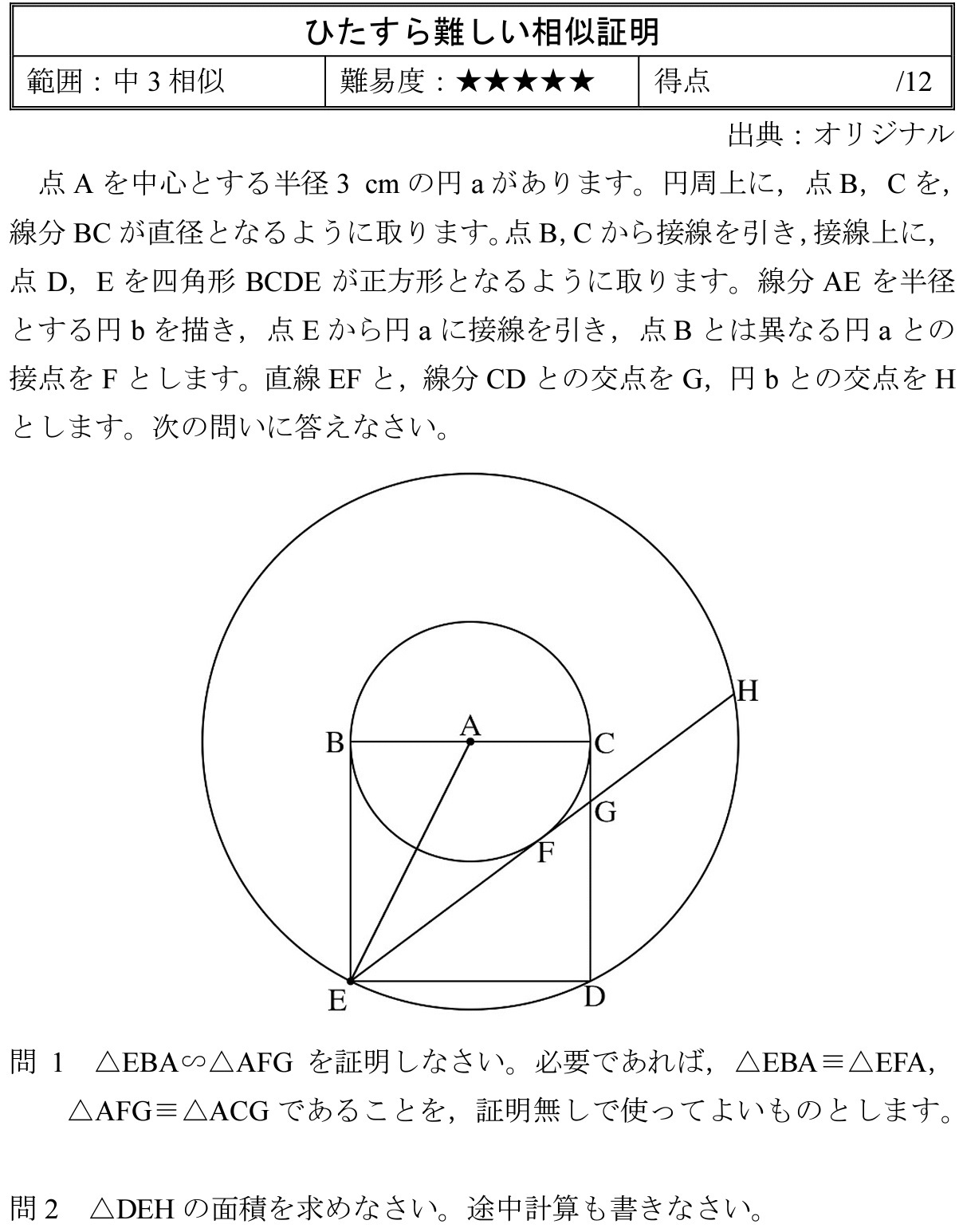



ひたすら難しい相似証明 オリジナル 高校入試 数学 良問 難問



三角形の相似の証明 平行線の錯角 勉強ナビゲーター



Studydoctor図形の性質と相似の証明 中3数学 Studydoctor



19年前期 千葉県公立高校入試 数学 第4問 図形の証明 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




中学3年の数学 動画 相似の証明チャレンジ lv 1の問題 19ch
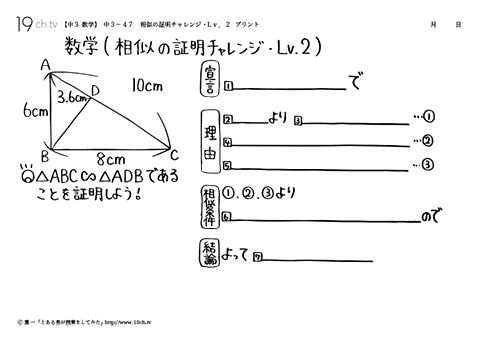



中学3年の数学 動画 相似の証明チャレンジ lv 2の問題 19ch
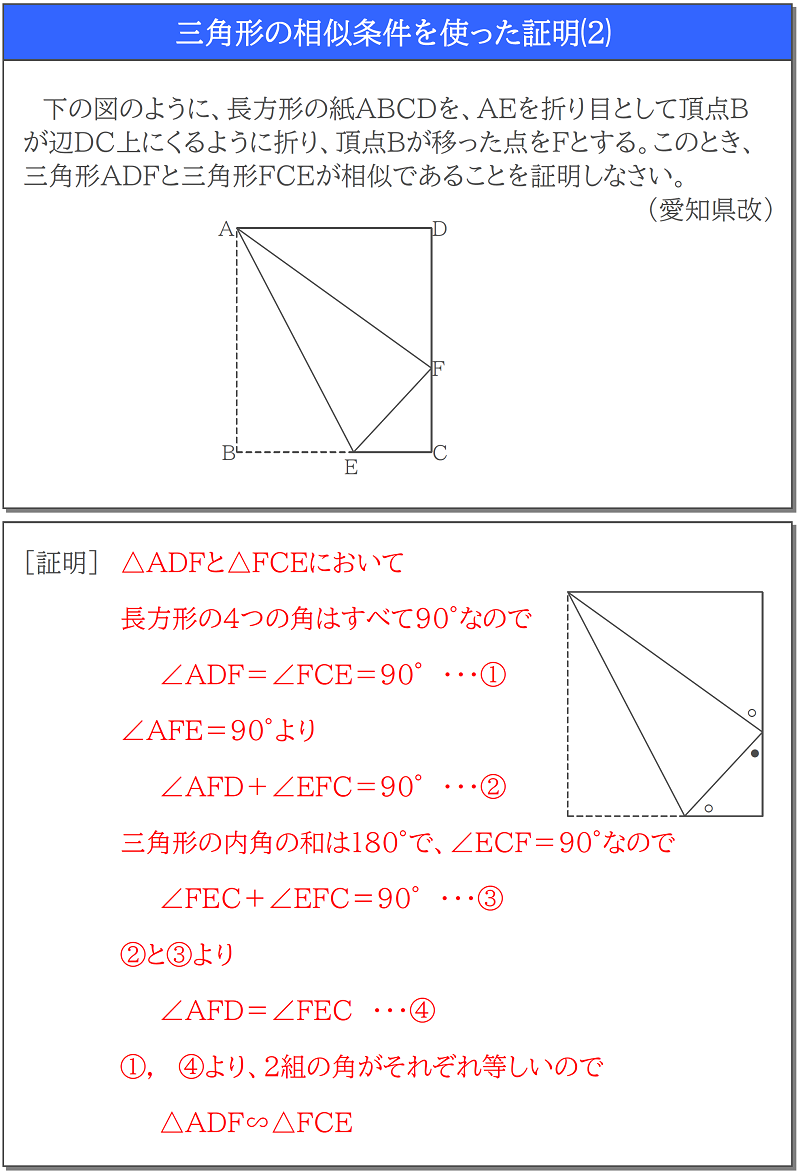



中学3年数学 相似条件を使った証明 2学期期末テスト 赤城 ᐡᐤᐡ




中三受験講座 英数ポイント解説映像授業 進研ゼミ中学講座会員サイト




これらの相似の証明の仕方が分かりません 解き方を教えてください 出来れば 相似の証明 Clear




5章1節2 三角形の相似条件2 数学のすすめ
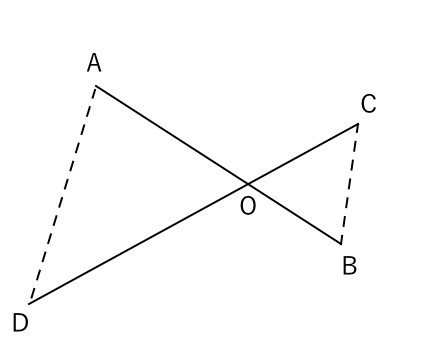



相似な図形 証明に慣れよう 苦手な数学を簡単に




この3問がどうしても わかりません 回答お願いいたします もしよければ途中経過も Clear




中三受験講座 英数ポイント解説映像授業 進研ゼミ中学講座会員サイト



三角形の相似条件 ドリるーむ



図形と証明 相似 無料学習プリント教材



3分でわかる 三角形の相似の性質と条件 証明問題の解き方 合格サプリ



中3数学 図形と相似8 相似条件と証明 折り返した図形 すべて無料 星組の中学数学講座




中3数学 図形と相似9 相似条件と証明 折り返しの図形 すべて無料 星組の中学数学講座



1
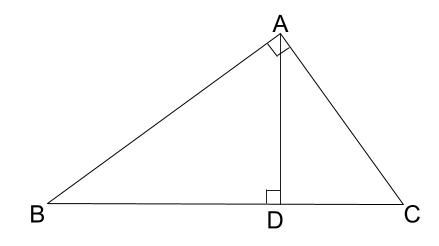



中学数学 相似の証明 その2 中学数学の無料オンライン学習サイトchu Su




世界一わかりやすい数学問題集中3 5章 図形と相似



14年前期 千葉県公立高校入試 数学 第4問 図形の証明 配点15点 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




円と相似 無料で使える中学学習プリント




中学3年の数学 動画 相似の証明チャレンジ lv 3の問題 19ch




三角形の相似条件と証明問題の解き方 数学fun
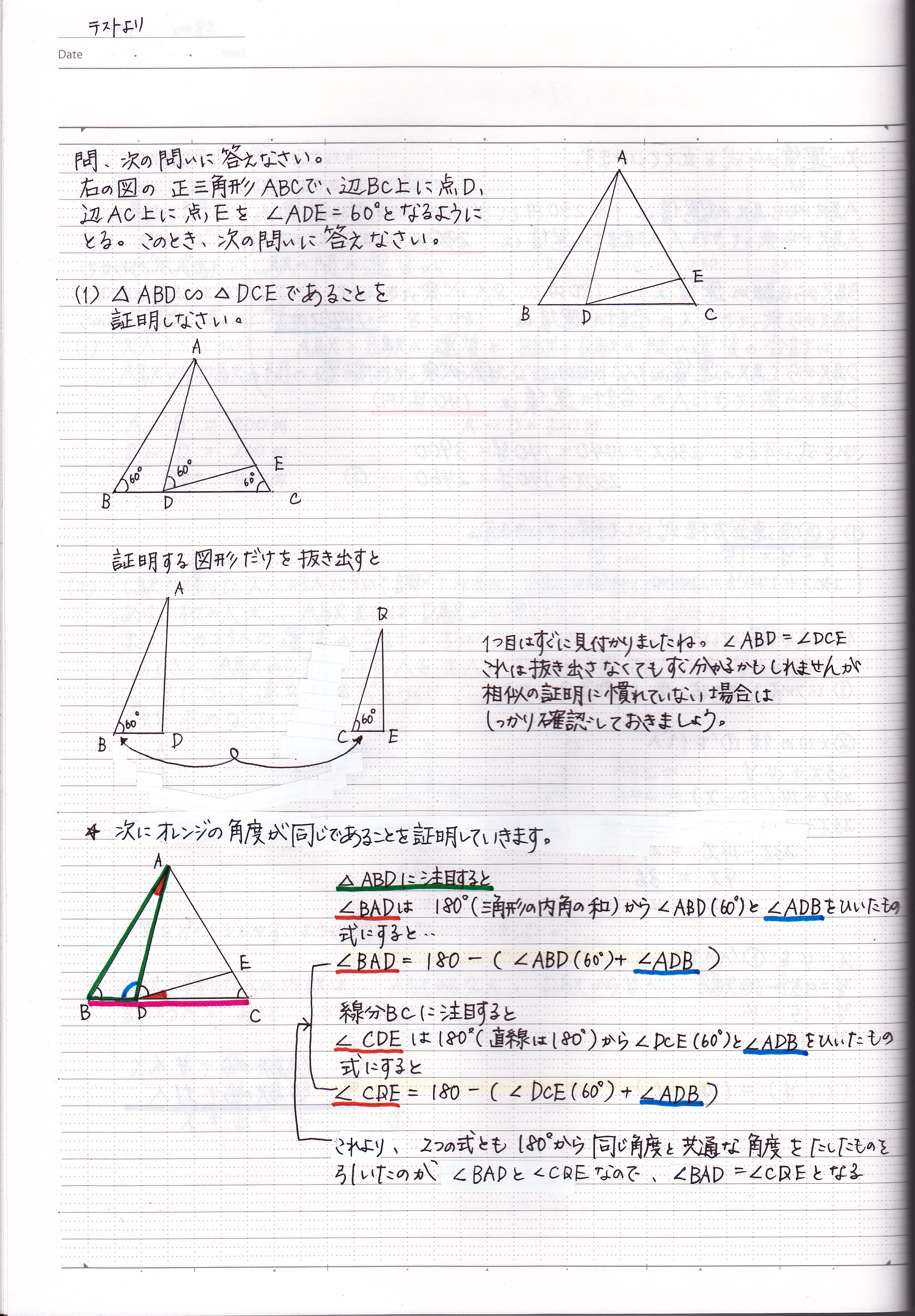



三角形の相似の証明の解き方 現役塾講師のわかりやすい中学数学の解き方
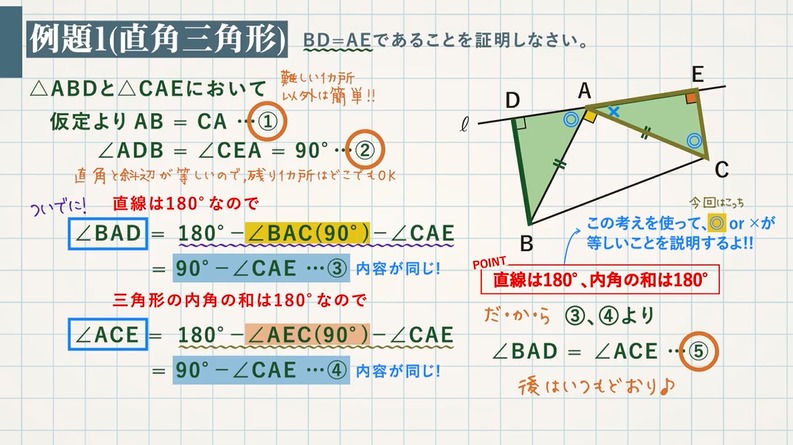



考え方はまったく同じ 合同 相似の証明でよく出る応用問題 教遊者




相似な図形の面積比の問題 相似比を出してから二乗しよう 中学や高校の数学の計算問題



三角形の相似条件と有名な例題3問 具体例で学ぶ数学




中学3年 数学 東京書籍 新しい数学 相似な図形 平行線と比 赤城 ᐡᐤᐡ



中3数学 パターン確認 円周角と相似 個別指導塾のyou 学舎日記 公式ブログ




相似の証明04 Geogebra




中3数学 相似の証明問題 練習編 映像授業のtry It トライイット




まるは気にしないで下さい この書き方で正解ですか Clear



中学校数学 証明のコツ 相似




中3数学 円と相似 の証明問題の解き方のコツ 映像授業のtry It トライイット



1




平行線と相似 証明 Youtube



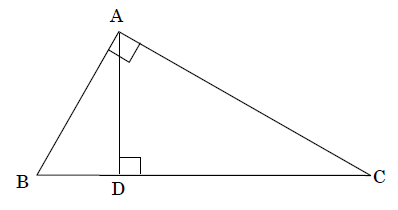
直角三角形の相似条件 具体例で学ぶ数学




無料 中3数学 基本問題 解答プリント 図形の相似2 相似条件と証明



直角三角形の相似条件 具体例で学ぶ数学




円周角の定理を使った相似の証明の解き方 現役塾講師のわかりやすい中学数学の解き方



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス




中学数学 よく出る円と相似の融合問題 Pikuu




相似の証明 チーム エン
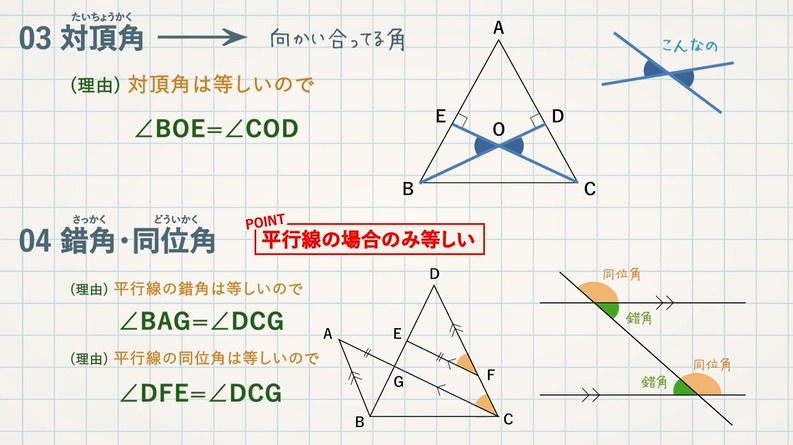



証明 合同 相似 が苦手な人へ 教遊者




中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学




5章1節2 三角形の相似条件2 数学のすすめ




相似の証明2 チーム エン




いろいろな相似の証明 無料で使える中学学習プリント




三角形の相似条件が見やすい図で一発理解できる 練習問題付き 高校生向け受験応援メディア 受験のミカタ



0 件のコメント:
コメントを投稿